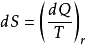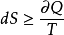物理定義：熵增過程是一個自發的由有序向無序發展的過程(Bortz, 1986; Roth, 1993)。 熱力學定義：熵增加，系統的總能量不變，但其中可用部分減少。統計學定義：熵衡量系統的無序性。熵越高的系統就越難精確描述其微觀狀態。
早在1943年，在愛爾蘭都柏林三一學院的多次演講中，薛丁格就指出了熵增過程也必然體現在生命體系之中，其於1944年出版的著作《生命是什麼》中更是將其列為其基本觀點，即“生命是非平衡系統並以負熵為生。”人體是一個巨大的化學反應庫，生命的代謝過程建立在生物化學反應的基礎上。從某種角度來講，生命的意義就在於具有抵抗自身熵增的能力，即具有熵減的能力。在人體的生命化學活動中，自發和非自發過程同時存在，相互依存，因為熵增的必然性，生命體不斷地由有序走回無序，最終不可逆地走向老化死亡。
基本介紹
- 中文名：熵增
- 外文名：increase of entropy
- 領域：熱力學
- 性質：自發的由有序向無序發展的過程
- 基本原理：熵增原理
- ：
熵的定義,熱力學定義,統計學定義,熵介紹,熵的定義,熵的性質,熵增原理,化學熱力學,
熵的定義
熱力學定義
統計學定義
在統計學中，熵衡量系統的無序性，代表了系統在給定的巨觀狀態（如溫度、壓強、體積等等）下，處於不同微觀狀態的可能性，或者說構成該巨觀系統的微觀方式的數量。舉例，已知在3個盒子裡有3個球，這個是系統的巨觀狀態，微觀狀態則是球在不同盒子間的分布（如3個球全部在第一個盒子，或者一個盒子裡有一個球等等）。熵越高的系統就越難精確描述其微觀狀態。
熵介紹
熵的定義
熵，熱力學中表征物質狀態的參量之一，用符號S表示，其物理意義是體系混亂程度的度量。
（1）經典熱力學
1865年，克勞休斯將發現的新的狀態函式命名為熵，用增量定義為
，式中T為物質的熱力學溫度；dQ為熵增過程中加入物質的熱量。
若過程是不可逆的，則
，下標“ir”是英文單詞“irreversible‘’的縮寫，表示加熱過程所引起的變化過程是不可逆的。
合併以上兩式可得
，此式叫做克勞休斯不等式，是熱力學中第二定律最普遍的表達式。
（2）統計熱力學
熵的大小與體系的微觀狀態Ω有關，即S=klnΩ，其中k為玻爾茲曼常量，k=1.3807x10-23J·K-1。體系微觀狀態Ω是大量質點的體系經統計規律而得到的熱力學機率，因此熵有統計意義，對只有幾個、幾十或幾百分子的體系就無所謂熵。
熵的性質
（1）狀態函式
熵S是狀態函式，具有加和（容量）性質（即對於系統M可分為M1與M2，則有SM=SM1+SM2），是廣度量非守恆量，因為其定義式中的熱量與物質的量成正比，但確定的狀態有確定量。其變化量ΔS只決定於體系的始終態而與過程可逆與否無關。由於體系熵的變化值等於可逆過程熱溫商δQ/T之和，所以只能通過可逆過程求的體系的熵變。孤立體系的可逆變化或絕熱可逆變化過程ΔS=0。
（2）巨觀量
熵是巨觀量，是構成體系的大量微觀離子集體表現出來的性質。它包括分子的平動、振動、轉動、電子運動及核自旋運動所貢獻的熵，談論個別微觀粒子的熵無意義。
（3）絕對值
熵的絕對值不能由熱力學第二定律確定。可根據量熱數據由第三定律確定熵的絕對值，叫規定熵或量熱法。還可由分子的微觀結構數據用統計熱力學的方法計算出熵的絕對值，叫統計熵或光譜熵。
熵增原理
熵增原理就是孤立熱力學系統的熵不減少，總是增大或者不變。用來給出一個孤立系統的演化方向。說明一個孤立系統不可能朝低熵的狀態發展即不會變得有序。
系統經絕熱過程由一狀態達到另一狀態熵值不減少——熵增原理（the principle of the increase of entropy）
對絕熱過程，Q = 0 ，有ΔS（絕熱）≥ 0（大於時候不可逆，等於時候可逆） 或 dS（絕熱）≥0 (>0不可逆；=0可逆)
熵增原理表明，在絕熱條件下，只可能發生dS≥0 的過程，其中dS = 0 表示可逆過程；dS>0表示不可逆過程,dS<0 過程是不可能發生的。但可逆過程畢竟是一個理想過程。因此，在絕熱條件下，一切可能發生的實際過程都使系統的熵增大，直到達到平衡態。
玻爾茲曼曾經通過仔細研究兩個球形分子碰撞前與碰撞後的景象，宣稱能證明碰撞前的熵小於撞後的熵，因此熵在增加。但是他的證明是錯的，原因是如果是這樣，同樣的論證過程可以運用在時間的反方向上，那么也應該是熵增，時間反方向上熵增，也就說明正方向上是熵減。
化學熱力學
在化學中，一般認為大部分化學反應都是一定條件下可逆的，換言之“可以從前向後也可以從後向前”。事實上，一定條件下化學反應的方向判定並非易事。在已知焓變不足以確定化學反應方向時，為了確定一定條件下化學反應的方向，熱力學定義“熵”被引入了化學中。由熵增原理可以推導出，化學反應向著“混亂度增大”，熵增大的方向進行，即趨向於ΔrS>0。(r為英語單詞reacting的詞頭，意思是化學反應中)
但是實際計算中，由於狀態數Ω不可直接求得，僅僅依靠熵的定義式S=klnΩ是無法確定熵變的。此時需要另外一個公式：ΔS=Qr/T。此處ΔS為熵變，Qr為熱量，T為熱力學溫度，單位為K。依靠這個公式可以計算出反應的熵變，從而判斷化學反應的方向，但是計算較為困難，在不恆溫時利用此式運算需要用到積分的數學手法。
我們知道給定環境中體系的熵是固定的，因此人們把在298K時1mol某種物質的熵稱為“標準摩爾熵”，即“標準熵”。符號為SmΘ（Θ讀作“西塔”，意思是標準狀況）。比如，SmΘH2(g)=130.57J/(mol·K)。由標準熵我們可以求得化學反應的標準摩爾熵變ΔrSmΘ：
ΔrSmΘ=∑viSmΘ（生成物）-∑viSmΘ（反應物）
此外，由ΔS=Qr/T可看出ΔS受T變化影響較小，因此在情況需要時可以直接將標準熵套入計算。
利用求得的摩爾熵變與焓變，可以通過ΔG=ΔH-TΔS計算出反應的吉布斯自由能降低量，設反應所做的非體積功為W，則
1.若W+ΔG<0，反應不可逆自發進行；
2.若W+ΔG=0，反應可逆進行；
3.若W+ΔG>0，反應無法進行。
由此可以準確無誤判斷一定條件下化學反應是否進行，這就是熵與熵增在化學熱力學中的套用。
