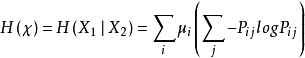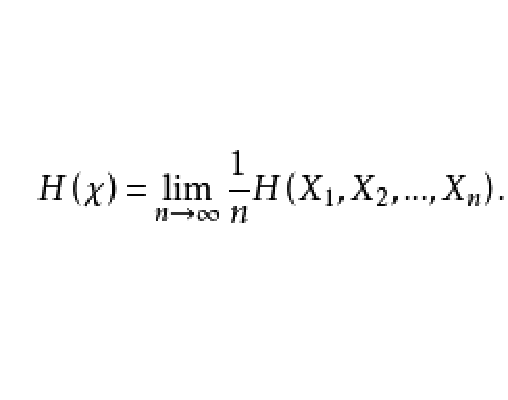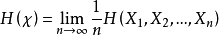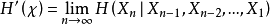熵的概念是由資訊理論的創始人申農(Shannon)提出的,在統計學中用它作為隨機事件不確定程度的一種度量,描述給定長度為n的隨機變數序列的熵隨n的增長情況。
基本介紹
- 中文名:熵率
- 外文名:Entropy rate
- 所屬學科:數學
- 研究對象:隨機變數序列
- 意義:對隨機事件不確定程度的一種度量
基本介紹,定義,舉例說明,重要定理,定理1,定理2,定理3,定理4,
基本介紹
定義
當如下極限存在時,隨機過程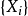 的熵率定義為
的熵率定義為
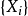
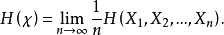
舉例說明
下面考慮幾個簡單的隨機過程例子及其相應的熵率。
1.打字機。假定一台打字機可輸出m個等可能的字母。由此打字機可產生長度為n的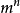 個序列,並且都等可能出現。因此,
個序列,並且都等可能出現。因此,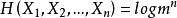 ,熵率為
,熵率為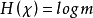 比特/字元。隨機過程的熵率43符。
比特/字元。隨機過程的熵率43符。
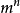
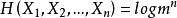
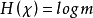
2.i.i.d. 隨機變數序列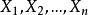 。此時,有
。此時,有
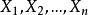
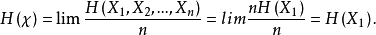
3.獨立但非同分布的隨機變數序列。在此情形下,有
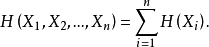
但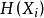 不全相等。我們可以選擇
不全相等。我們可以選擇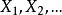 的一個分布序列,使
的一個分布序列,使 的極限不存在。例如取二值隨機分布序列,其中
的極限不存在。例如取二值隨機分布序列,其中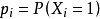 不是常數,而為i的函式。通過細心選取
不是常數,而為i的函式。通過細心選取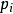 匕糾可使得式
匕糾可使得式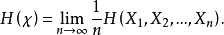 的極限不存在。例如,對
的極限不存在。例如,對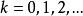 取
取
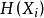
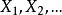

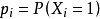
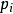
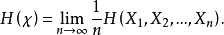
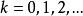
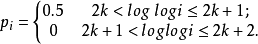
此時,該序列的情況是,滿足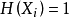 的隨機變數序列(可以任意長)之後,緊接著是更長以指數變化的序列滿足
的隨機變數序列(可以任意長)之後,緊接著是更長以指數變化的序列滿足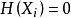 。所以,
。所以,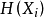 的累積平均值將在0與1之間振盪,從而不存在極限。因此,該過程的
的累積平均值將在0與1之間振盪,從而不存在極限。因此,該過程的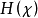 無定義。
無定義。
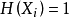
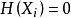
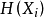
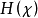
我們也可以定義熵率的一個相關的量(如果下列極限存在):
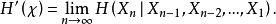
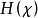
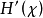
重要定理
定理1
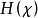
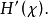
我們先來證明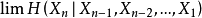 存在。
存在。
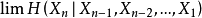
定理2
對於平穩隨機過程,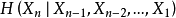 隨n遞減且存在極限
隨n遞減且存在極限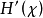 。
。
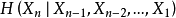
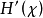
證明:
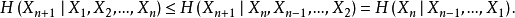
其中的不等式由條件作用使熵減小這個性質得到,而等式由該過程的平穩性得到。由於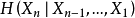 是非負且遞減的數列,故其極限
是非負且遞減的數列,故其極限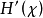 存在。
存在。
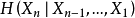
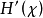
接下來使用數學分析中的一個如下簡單結論。
定理3
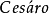

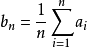
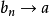
證明:(非正式思路)由於序列 中的大部分項最終趨於a,那么,
中的大部分項最終趨於a,那么,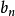 是
是 的前n項的平均,也將最終趨於a。正式證明閱參考資料。
的前n項的平均,也將最終趨於a。正式證明閱參考資料。

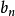

定理1的證明 由鏈式法則
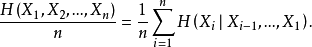
也就是說,熵率為條件熵的時間平均。然而,我們已經知道條件熵趨於極限H',因此,由定理3可知,條件熵的累積平均存在極限,且此極限就是其通項的極限H'。於是,由定理2,
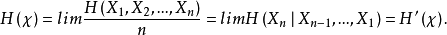
研究隨機過程熵率的重要意義體現在平穩遍歷過程的AEP。
對任何平穩過程,熵率均有恰當的定義。而對於馬爾可夫鏈,計算熵率尤為容易。
馬爾可夫鏈對於平穩的馬爾可夫鏈,熵率為
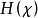
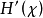
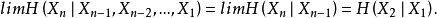
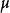
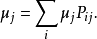
其中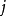 為任意值。
為任意值。
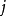
定理4
設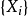 為平穩馬爾可夫鏈,其平穩分布為
為平穩馬爾可夫鏈,其平穩分布為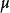 ,轉移矩陣為P。則熵率為
,轉移矩陣為P。則熵率為
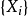
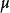
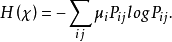
證明: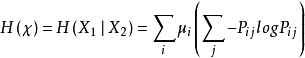 。
。