設A是R的子集,則A按R中的距離ρ也成內度量空間,稱為R的(度量)子空間。
基本介紹
- 中文名:度量子空間
- 外文名:metric subspace
- 適用範圍:數理科學
簡介
度量空間
定義
相關概念

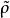
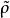
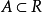
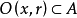
設A是R的子集,則A按R中的距離ρ也成內度量空間,稱為R的(度量)子空間。

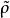
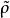
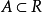
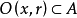
設A是R的子集,則A按R中的距離ρ也成內度量空間,稱為R的(度量)子空間。...... 設A是R的子集,則A按R中的距離ρ也成內度量空間,稱為R的(度量)子空間。...
度量空間(Metric Space),在數學中是指一個集合,並且該集合中的任意元素之間的距離是可定義的。亦稱距離空間。一類特殊的拓撲空間。弗雷歇(Fréchet,M.-R.)將...
度量線性空間(metric linear space)是一類定義了距離的線性空間。設E是線性空間,又是度量空間,ρ是E上的距離,且E按ρ導出的拓撲成為拓撲線性空間,則稱E為度量...
度量空間(MetricSpace),在數學中是指一個集合,並且該集合中的任意元素之間的距離是可定義的。...
則稱ρ(x,y)為兩點x,y之間的距離,R按距離ρ成為度量空間或距離空間,記為(R,ρ)。設A是R的子集,則A按R中的距離ρ也成為度量空間,稱為R的(度量)子空間...
可度量化空間(metrizable space)是一類特殊的拓撲空間,設X是拓撲空間,若在集合X上存在一個度量d,使得X上由d誘導的拓撲和X上原來的拓撲一致,則稱X為可度量化...
完備空間或者完備度量空間是具有下述性質的空間:空間中的任何柯西序列都收斂在該空間之內。以有限維空間來說,向量的範數相當於向量的模的長度。但是在有限維歐式空間...
商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。...... 賦范線性空間(normed linear space)是線上性空間中引進一種與代數運算相聯繫的度...
在數學領域線性代數和泛函分析中,內積空間 V 的子空間 W 的正交補是正交於 W 中所有向量的所有 V 中向量的集合。...
《相關性度量技術及其在圖像處理中的套用》主要研究相關性定量度量技術及其在圖像...5.4.1遞歸子空間融合方案 5.4.2實驗及結果分析 5.5融合結構對圖像融合性能...
度量空間是弗雷歇(Fréchet,M.-R.)於1906年引進的,它是現代數學中的一種基本而重要並且非常接近於歐幾里得空間的抽象空間,也是泛函分析的基礎之一。勒貝格數(...
度量空間亦稱距離空間。一種拓撲空間,其上的拓撲由距離決定。可擴映射(expansive map)是一類重要的動力系統。設(M,d)是一個度量空間,f:M→M是一連續映射,如果...
設A是R的子集,則A按R中的距離ρ也成內度量空間,稱為R的(度量)子空間。擬距離定義 如果把上述距離的條件1改為ρ(x,y)≥0且ρ(x,x)=0,則稱ρ為R上...
1 概念 2 穩定性 3 度量空間 4 同胚 5 實例——擴張映射 拓撲穩定性概念 編輯 拓撲穩定性(topological stability)亦稱半結構穩定性或半穩定性。通常...
