平衡分布是指熱力學系統達到平衡後,組成系統的N個粒子在粒子許可能級上的分布。
基本介紹
- 中文名:平衡分布
- 外文名:equilibrium distribution
- 領域:統計學
- 研究對象:微觀粒子
- 條件:熱力學平衡
定義
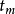

舉例論證
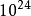
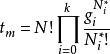


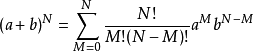
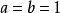
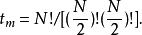

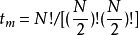
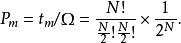
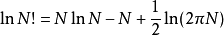
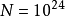
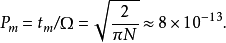


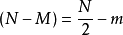
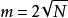
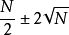
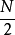
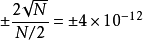
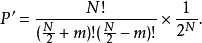
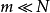


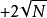
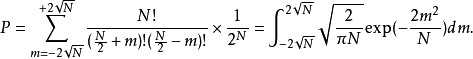
平衡分布是指熱力學系統達到平衡後,組成系統的N個粒子在粒子許可能級上的分布。
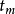

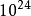
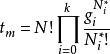


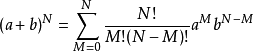
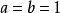
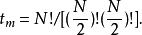

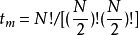
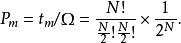
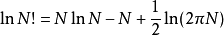
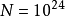
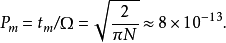


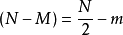
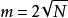
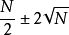
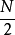
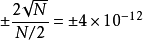
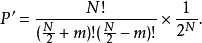
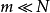


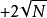
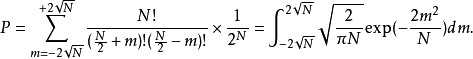
平衡分布是指熱力學系統達到平衡後,組成系統的N個粒子在粒子許可能級上的分布。... 平衡分布是指熱力學系統達到平衡後,組成系統的N個粒子在粒子許可能級上的分布。...
最可幾分布就是微態數最大的分布,那么,是否可用最可幾分布來表示巨觀的平衡狀態!一個巨觀系統的平衡狀態即是微觀狀態數最多的狀態。 在NUV確定的系統達平衡時,...
統計平衡(statistical equilibrium)是指當組成系統的子系按微觀運動狀態的分布等於給定巨觀條件下的最概然分布時系統所處的狀態。...
玻爾茲曼分布也叫吉布斯分布,是一種覆蓋系統各種狀態的機率分布、機率測量或者頻率分布。當有保守外力(如重力場、電場等)作用時,氣體分子的空間位置就不再均勻分布了...
本書系統地論述了水溶組分平衡分布的計算方法及其在水文地質領域的套用,全書共分七章,在介紹了化學熱力學基本理論的基礎上詳細闡述了水溶組分平衡分布的含義及其計算...
分布係數(也稱分配係數),分析化學概念之一。所謂分配定律是指一定溫度下,物質A在兩種互不相溶的溶劑中達到分配平衡時在兩相中的活度(常近似為濃度)之比,即分配...
玻色-愛因斯坦分布是指無相互作用自旋為整數的量子粒子在諸能級(E)上平均粒子占有數的平衡分布。...
核統計平衡理論是指該理論假設,在宇宙之初,物質以高溫和高密度狀態存在,從而導致核轉變迅速發生,達到- 種真正的統計平衡分布。這時核A和核B結合形成核C和核D的...
平衡更新過程(equilibrium renewal process),是一類特殊的延遲更新過程。... 其中產是其餘更新間距的共同分布F的數學期望.這類過程的得名是由於F*是F的平衡分布....
平衡原理(equilibrium principle)是靜電學中平衡問題的數學描述。在經典位勢論中,平衡問題(即對經典位勢如何確定上述的測度μ)與掃除問題、狄利克雷問題被列為位勢...
資源平衡簡稱“平衡”。亦稱“有限資料進度計畫"。當資源成為制約項目進度計畫的因素時,所採用的分析方法。將資源有效分配到項目活動中,其目的是減少資源過度分配,...
平衡態(equilibrium state)是指在沒有外界影響條件下熱力學系統 的各部分巨觀性質在長時間裡不發生變化的狀態。這裡所說的沒有外界影響,是指系統與外界沒有相互...
人口分布是指人口在一定時間內的空間存在形式、分布狀況,包括各類地區總人口的分布,以及某些特定人口(如城市人口、特定的人口過程和構成(如遷移、性別等)的分布等。...
職住平衡的基本內涵是指在某一給定的地域範圍內,居民中勞動者的數量和就業崗位的數量大致相等,即職工的數量與住戶的數量大體保持平衡狀態,大部分居民可以就近工作;...
平衡態與非平衡態是對於某個物理量,在系統內部的各處相等、均勻分布,則稱系統在巨觀上呈現出的完全均勻狀態為系統的平衡態。反之,則稱之為非平衡態。這些物理量...
平衡孔是指在葉輪的後蓋板上靠近輪轂的地方開一圈小孔(平衡孔),以使葉輪背面環形室保持恆定的低壓。為減少泄露,在葉輪後蓋板也裝上密封環,其半徑位置與吸入口的...
機率分布評估模型就是對相關水平的消費量及其所評價化學物在食品中的存在與污染水平(濃度)進行模擬。在機率分模型中至少有一個變數是由分布函式構成。此評估方法相比...
熱量平衡是一個物體或系統的熱量收支相等時的狀況。對地球表面、大氣和地-氣系統的熱量收支關係的研究是物理氣候學的重要課題之一。輻射差額及其轉變的其他熱量消耗...
平衡針灸學是以心理、生理、社會、自然相適應的整體醫學調節模式,充分利用人體的信息系統(即神經、經絡與體液系統》 和針刺技術的反饋效應原理,以針刺為手段,選擇...
資金平衡結構指資金平衡表的結構。資金平衡表一般分為左右兩方,左方列示資金占用 (或資金運用) 項目,反映資金分布情況; 右方列示資金來源項目,反映資金取得的渠道...
玻色愛因斯坦分布是指熱平衡狀態下,全同玻色子(自旋為整數或零的粒子)相對於能量狀態的統計分布。...
平衡式傳輸線指傳輸線體系中的訊號線,是由兩條並行線併合而成。這種平衡電路 (Balanced Circuit ) 也稱為 "差動線對" ( Differential Pair) 或差動線 ( ...
開展企業電能平衡測試工作,是全面系統摸清企業的電力、電量消耗總量、構成、分布、流向、用電設備的狀況和電能利用率,是加強能源科學管理、制訂節電規劃、確定節能技措...
迴轉平衡分為動平衡和靜平衡,由於迴轉件的結構形狀不對稱、製造安裝不準確或材質不均勻等原因,在轉動時產生的離心力和離心力偶矩不平衡,致使迴轉件內部產生附加應力...
遺傳平衡是群體遺傳學的基本概念,根據遺傳平衡理論,可以估計遺傳學參數,檢查遺傳學假說,又可由此出發,研究各種進化現象。基因頻率在突變、自然選擇,基因漂變等壓力下...
由於地殼運動的不平衡性,地球上各種岩石分布也是不均勻的,因而造成了各種礦產資源在地理分布上的不均衡狀態。許多礦產存在於局部高度富集區。...
