在指定N、U、V 條件下,微觀狀態數最大的分布出現的機率最大,該種分布即稱為最概然分布.
基本介紹
- 中文名:最概然分布
- 外文名:most probable distribution
- 又名:最可幾分布
- 類別:數學現象
- 原理:等機率原理
- 學科:數學
解釋
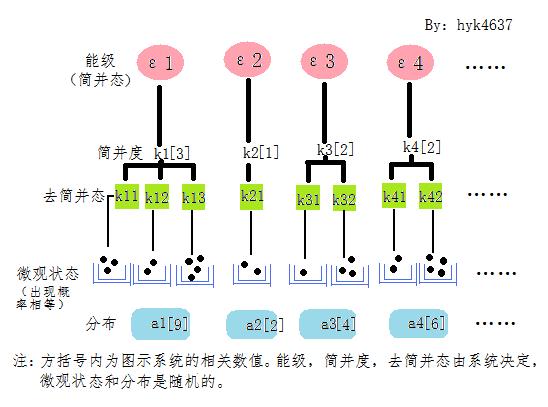 粒子分布圖
粒子分布圖關係
示例
級的兩個簡併量子態,因此,所有微觀狀態有相同的能量,他們都服從等機率原理。
由圖2 可見,隨著N 增大,分布曲線變得越來越窄,換句話說,平衡分布越來越接近最概然分布。
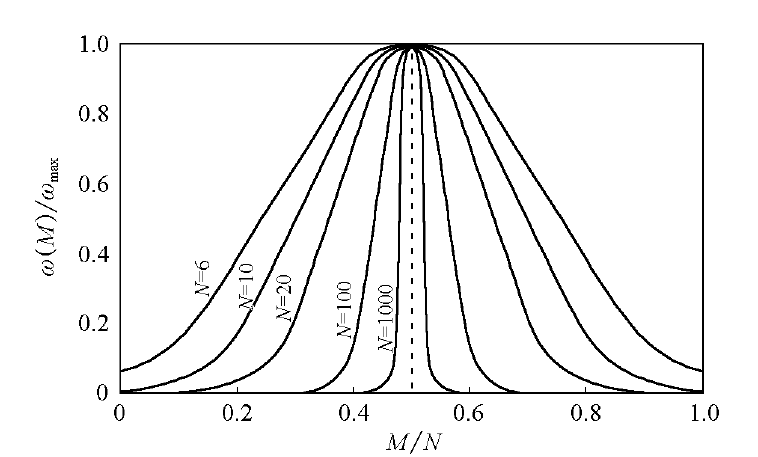 最概然分布
最概然分布
在指定N、U、V 條件下,微觀狀態數最大的分布出現的機率最大,該種分布即稱為最概然分布.
 粒子分布圖
粒子分布圖 最概然分布
最概然分布在指定N、U、V 條件下,微觀狀態數最大的分布出現的機率最大,該種分布即稱為最概然分布...
玻色分布,全同和獨立的玻色子系統中粒子的最概然分布。...... 玻色分布,全同和獨立的玻色子系統中粒子的最概然分布。玻色子是 自旋為整數( 即自旋為n*h/2π...
熱力學系統達到平衡後,組成系統的N個粒子在粒子許可能級上的分布稱之為平衡分布。波爾茲曼Boltzmann認為,當N足夠大時,系統平衡時的最概然分布就能代表系統平衡時的...
全同和獨立的費米子系統中粒子的最概然分布。簡稱費米分布,量子統計中費米子所遵循的統計規律。由E.費米和P.A.M.狄拉克在1926年先後提出,故名。...
費米-狄拉克分布(Fermi-Dirac distribution)全同和獨立的費米子系統中粒子的最概然分布。簡稱費米分布,量子統計中費米子所遵循的統計規律。這個統計規律的命名來源...
統計平衡(statistical equilibrium)是指當組成系統的子系按微觀運動狀態的分布等於給定巨觀條件下的最概然分布時系統所處的狀態。...
第二章 玻耳茲曼最概然分布 §2.1 力學規律性和統計規律性 §2.2 體系和粒子運動狀態的微觀描述μ空間 §2.3 玻耳茲曼最概然分布 §2.4 熱力學公式和熵 §...
14—11B—E分布函式 14—12光子統計普朗克黑體輻射公式 14—13聲子統計固體的比熱 附錄14—Ⅰ積分的計算 附錄14—Ⅱ平均速率均方根速率最概然速率速度分量在...
12.4 最概然分布 Ⅱ. 獨立子系統的統計分布 12.5 麥克斯韋-玻耳茲曼分布 12.6 子配分函式 Ⅲ. 獨立子系統的熱力學性質 12.7 獨立子系統的熱力學函式 12....
§9.6 最概然分布和-切分布§9.7 Maxwell速率分布定律§9.8 單粒子配分函式§9.9 統計分布律是體系狀態的統計描述§9.10 獨立子體系求統計平均值的公式參考...
8 3 2最概然分布578 4能級分布的微態數598 4 1定域子系統能級分布的微態數598 4 2離域子系統能級分布的微態數608 5玻爾茲曼統計61...
12.4 最概然分布Ⅱ.獨立子系統的統計分布12.5 麥克斯韋-玻耳茲曼分布12.6 子配分函式Ⅲ.獨立子系統的熱力學性質12.7 獨立子系統的熱力學函式...
7.1.6最概然分布與平衡分布1987.2玻爾茲曼分布律與粒子配分函式2017.2.1玻爾茲曼分布律2017.2.2粒子配分函式q2037.2.3粒子配分函式的計算2047.3配分函式...
全書共11章,內容包括:熱力學的基本規律,均勻物質的熱力學性質,單元系的相變,多元系的復相平衡和化學平衡,不可逆過程熱力學簡介,近獨立粒子的最概然分布,玻耳茲曼...
第六章 近獨立粒子的最概然分布 §6.1 粒子運動狀態的經典描述 §6.2 粒子運動狀態的量子描述 §6.3 系統微觀運動狀態的描述 §6.4 等機率原理.. §6.5 分...
第二章 最概然分布法 第三章 能斯特定理的討論 第四章 關於第二章的例子 (1)自由質點(單原子理想氣體) (2)普朗克振子 (3)費米振子 第五章 漲落 第六章...
最概然分布:對於N個粒子分布在 ε1, ~ ε M 共M個能級上會有多種分布,其中機率最大的分布.平衡分布: N,V,E確定的系統(N ≥ 1024)達到熱力學平衡時,...
機率分布,等機率原理,近獨立粒子系統計方法;第6章系綜理論;第7、8章系綜理論...5.7近獨立粒子系統的巨觀態分布與微觀狀態數5.8近獨立粒子系統的最概然分布習題...
4.4 近獨立粒子系統的分布和微觀狀態數 794.5 近獨立粒子系統的最概然分布 83習題及參考答案 86第5章 近獨立粒子系統的統計規律 88...
§8.5 玻爾茲曼分布——最概然分布 §8.6 求物理量的統計平均值 習題 第九章 熱力學量的統計表示 §9.1 熱力學第一定律和第二定律 §9.2 用配分函式表示...
在研究的問題中,會涉及粒子的相互作用,系統的能量表達式包含粒子間相互作用的勢能,不能利用最概然分布方法,系統理論可以研究互作用組成的系統。考慮一個系統在給定的...
1.3.1 微觀狀態及最概然分布1.3.2 統計分布函式1.4 多體體系的一種近似處理方法1.5 固體物理的兩個基本近似附錄1 A量子力學中的力學量...
第四節玻爾茲曼分布2441 最概然分布2442 玻爾茲曼分布246第五節玻色 愛因斯坦統計和費米 狄拉克統計2491 玻色 愛因斯坦統計2492 費米 狄拉克統計249...
