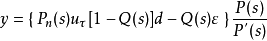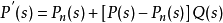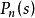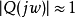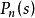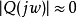基本原理
干擾觀測器的基本結構如圖。圖中的Gp(S)為對象的傳遞函式,d為等效干擾,
為觀測干擾,u為控制輸入。由圖可以求出等效干擾的估計值
為
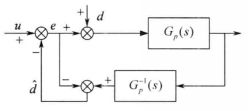 干擾觀測器的基本結構
干擾觀測器的基本結構對於實際的物理系統,其實現存在如下問題:
(1)通常情況下,Gp(s)的相對階不為零,其逆在物理上難以實現。
(2)對象Gp(s)的精確數學模型無法得到。
(3)考慮到測量噪聲的影響,該方法的控制性能將下降。
解決上述這些問題的唯一方法是在
的後面串人低通濾波器Q(s),並用名義模型
的逆
來代替
,從而得到如圖所示的干擾觀測器框圖,其中虛線框部分為干擾觀測器。
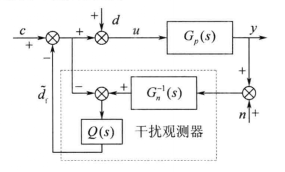 干擾觀測器原理框圖
干擾觀測器原理框圖控制器的輸出為
式中:c為改進的變飽和狀態柔性變結構控制器的輸出;
為干擾d的估計值;n為感測器的等效測量誤差。由上式可知,當干擾觀測器預測得到的干擾也等於系統干擾d時,改進的變飽和狀態柔性變結構控制器的輸出即為系統的控制輸入,干擾對系統的影響被降低到最小。由圖可知,
通過低通濾波器Q(s)的設計可較好地抵抗外加干擾。由上面的分析可見,
Q(s)的設計是干擾觀測器設計中的一個重要環節。首先,為使
正則,Q(s)的相對階應不小於
的相對階;其次,Q(s)頻寬的設計應是在干擾觀測器的魯棒穩定性和干擾抑制能力之間的折中。
設
的名義模型為
,則不確定對象的集合可以用乘積攝動來描述,即
式中
為可變的傳遞函式。在仿真時,可設
是一個固定的等效誤差值,也可設定為一個變化的隨機值,它表示實際對象模型對於名義模型的攝動。
由魯棒穩定性定理,干擾觀測器魯棒穩定的充分條件是
上式是Q(s)設計的基礎,通過Q(s)的設計,可實現魯棒性要求。忽略非建模動態不確定性的影響,對一個二階系統
常可描述為
。式中,
為等效慣性力矩;
為等效阻尼係數。
採用的Q(s)結構的標準形式為
選擇不同的
值,Q(s)濾波器對應不同的截止頻率
。增加
的值可以增加Q(s)的頻寬,而且能夠更加有效地抑制干擾。但是隨著
的增加,系統的穩定性會降低,甚至導致系統不穩定。因此,
的選擇要兼顧到系統的穩定性和抗干擾效果。理論上Q(s)的階數越高,系統的動態性能就越好,但會出現不穩定的問題。
改進的干擾觀測器設計
干擾觀測器在對干擾進行估計時,不需要對於擾信號建立準確的數學模型,而且它本身的結構也比較簡單,因此在預測干擾信號時避免了大量的數學計算,這有利於滿足實時性的要求。在系統設計時,考慮到系統的干擾可以歸結為外部擾動以及由於執行機構和其理想數學模型之間的參數變化而產生的誤差。因此,如果能夠利用干擾觀測器對干擾信號進行有效的預測並加以補償,那么在一定的誤差範圍內就可以將實際執行機構的模型用其參考模型來等價。
參考干擾觀測器的基本原理圖,並根據所要控制系統的特點,對圖二中的干擾觀測器作了改進,其結構如圖三所示。 圖三中,
為參考輸入,u為控制器輸出,d為系統的外部干擾,
為感測器的等效測量誤差,
為干擾觀測器的輸出即預測到的系統干擾。
由圖6.5可得系統的輸出y的表達式如下:
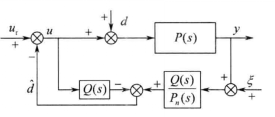 圖三改進的干擾觀測結構圖
圖三改進的干擾觀測結構圖式中
,假定P(s)代表實際執行機構,
為其參考模型,Q(s)為干擾觀測器的低通濾波器。當低於Q(s)的截止頻率即處於低頻段時,如果取
,那么P(s)的輸人輸出特性就等價於其理想參考模型屍。
的輸人輸出特性;當高於Q(s)的截止頻率時,如果取
,那么就會減小感測器的高頻測量誤差對系統的影響。因此,干擾觀測器設計的關鍵是其低通濾波器參數的選擇。
低通濾波器的性能決定整個干擾觀測器的動態特性。從理論上分析,如果Q(s)的頻寬越寬,階數越高,那么干擾觀測器的回響速度就越快,對干擾的抑制效果就越好,干擾對系統的影響越小即系統對干擾的靈敏度越低。但是隨著階數的升高,由於大的相位滯後使系統產生欠阻尼現象,甚至使系統變得不穩定。因此,如何使干擾觀測器獲得好的動態特性和高的穩定性是Q(s)設計的關鍵。
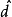
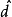
 干擾觀測器的基本結構
干擾觀測器的基本結構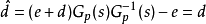
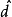
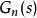
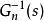
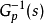
 干擾觀測器原理框圖
干擾觀測器原理框圖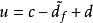
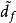
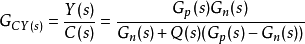
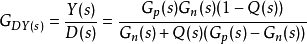
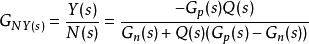
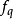
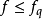
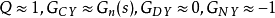
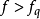
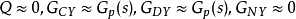
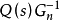
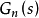
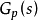
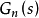
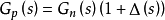
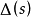
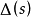
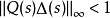
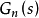
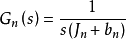
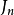
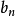
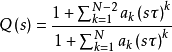

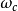
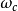
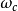
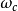
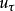

 圖三改進的干擾觀測結構圖
圖三改進的干擾觀測結構圖