基本介紹
- 中文名:差分運算元
- 外文名:difference operator
- 所屬學科:數學
- 表達式:Δf(x)=f(x+1)-f(x)
- 符號:Δ為向前差分運算元,簡稱差分運算元
基本概念







相關概念
















差分運算元的若干性質


套用舉例
Taylor級數


指數函式



二項式定理









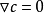
















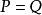
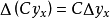








差分運算元是一種運算元,對任一實函式f(x),若記Δf(x)=f(x+1)-f(x),則稱Δ為向前差分運算元,簡稱差分運算元。差分是計算數學的基本概念之一,指離散函式在...
差分,又名差分函式或差分運算,差分的結果反映了離散量之間的一種變化,是研究離散數學的一種工具,常用函式差近似導數。差分在數學、物理和信息學中套用很廣泛,...
差分對應離散的運算,差分計算是使用差分進行的運算。...... ,簡稱為函式y(t)的(一階)差分,並稱D為差分運算元。差分計算套用 編輯 在比較兩個分數大小時,用...
差分格式是數值計算方法中微分以及偏微分導數的一種離散化方法,即用相鄰兩個或者多個數值點的差分取代偏微分方程中導數或者偏導數的一種算法。 選擇差分格式是...
中心差分格式,就是界面上的物理量採用線性插值公式來計算。在對流項中心差分的數值解不出現振盪的參數範圍內,在相同的格線節點數下,採用中心差分的計算結果要比...
設有序列f(k), 則稱...f(k+2),f(k+1),...f(k-1),f(k-2)...等為f(k)的移位序列 一階前向差分定義為 △稱為差分運算元; 二階前向差分定義...
在數學中,微分運算元是定義為微分運算之函式的運算元。首先在記號上,將微分考慮為一...差分運算元 Delta operator 橢圓型運算元 分數微積分 不變微分運算元 ...
Sobel運算元是像素圖像邊緣檢測中最重要的運算元之一,在機器學習、數字媒體、計算機視覺等信息科技領域起著舉足輕重的作用。在技術上,它是一個離散的一階差分運算元,用來...
在技術上,它是一離散性差分運算元,用來運算圖像亮度函式的梯度之近似值。在圖像的任何一點使用此運算元,索伯運算元的運算將會產生對應的梯度向量或是其範數。概念上,索...
其主要用於邊緣檢測,在技術上它是以離散型的差分運算元,用來運算圖像亮度函式的梯度的近似值,缺點是Sobel運算元並沒有將圖像的主題與背景嚴格地區分開來,換言之就是...
採用Sobel對腳印圖像的邊緣檢測可知,採用Sobel運算元對圖像進行邊緣檢測,紋理檢測效果一般,邊緣檢測斷斷續續,不具後續處理。Sobel運算元是一階離散性差分運算元, 用來運算...
Roberts運算元,又稱羅伯茨運算元,是一種最簡單的運算元,是一種利用局部差分運算元尋找邊緣的運算元。他採用對角線方向相鄰兩象素之差近似梯度幅值檢測邊緣。檢測垂直邊緣的效果...
Roberts邊緣檢測運算元是一種利用局部差分運算元尋找邊緣的運算元,Robert運算元圖像處理後結果邊緣不是很平滑。經分析,由於Robert運算元通常會在圖像邊緣附近的區域內 產生較寬的...
其主要用於邊緣檢測,在技術上它是以離散型的差分運算元,用來運算圖像亮度函式的梯度的近似值,缺點是Sobel運算元並沒有將圖像的主題與背景嚴格地區分開來,換言之就是...
據此,對數字圖像{f(i,j)}的每個像素,取它關於x軸方向和y軸方向的二階差分之和,表示為Laplacian運算元運算模板 編輯 函式的拉普拉斯運算元也是該函式的黑塞矩陣的跡...
興趣點運算元算法流程 1)利用水平,豎直差分運算元對圖像的每個像素進行濾波以求得Ix、Iy,進而求得M中的四個元素的值。2)對M的四個元素進行高斯平滑濾波,為的是...
微分定理 其中Df表示f的微分,如果在離散域中則是指差分運算元,包括前向差分與後向差分兩種。卷積卷積定理 卷積定理指出,函式卷積的傅立葉變換是函式傅立葉變換的...
