基本介紹
- 中文名:局部連通空間
- 外文名:locally connected space
- 學科:數學
- 屬性:一類拓撲空間
- 組成:連通子集組成的的鄰域基等
- 相關概念:連通空間、道路連通空間
定義
連通空間
局部連通空間
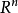

道路連通空間


與連通空間
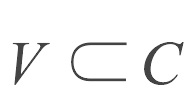
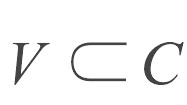

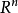



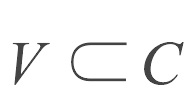
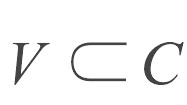
局部連通空間 (locally connected space),是一類拓撲空間,它由連通子集組成的的鄰域基及連通分支等組成。設X為拓撲空間X,若存在由連通子集組成的x的鄰域基,則稱...
連通性是‘點集拓撲學’中的基本概念,把‘連通性’定義如下:對於拓撲空間X,(1)若X中除了空集和X本身外,沒有別的既開又閉的子集,則稱此‘拓撲空間X是連通...
拓撲空間是一種數學結構,可以在上頭形式化地定義出如收斂、連通、連續等概念。拓撲空間在現代數學的各個分支都有套用,是一個居於中心地位的、統一性的概念。拓撲...
道路連通性保連通性,反之則不然。連通局部連通 編輯 一個拓撲空間被認為是局部連通的,如果空間中的每一點的任何一個鄰域都包含這個點的一個連通鄰域。這裡所說...
映射提升定理:若Y是連通且局部道路連通空間,r∈Y,(X~,p)是X的覆疊空間,a∈X,b∈p(a),則連續映射f:(Y,r)→(X,a)存在提升f~:(Y,r)→(X~,b)的...
若拓撲空間上任意兩點可由其上的弧連線(即此弧分別以這兩點為起點和終點),則稱此空間為弧連通的,若空間有一由弧連通集組成的基,則稱為局部弧連通空間。...
)}n, <X,二)是平凡同態,則稱X為半局部單連通的空間.泛覆疊空間的存在性定理:若X為連通、局部道路連通與半局部單連通的拓撲空間,則一定存在X的泛覆疊空間....
代數幾何的基本研究對象.它實際上就是一個局部同構於仿射概形的局部環空間.更...若概形X的拓撲空間是連通空間或不可約空間(即它不能表成兩個不同真閉子集...
4.3 連通分支4.4 局部連通空間4.5 道路連通空間第五章 有關可數性的公理5.1 第一與第二可數性公理5.2 可分空間第六章 分離性公理...
局部緊、第二可數空間,其他二者卻是.它們都是偽緊、局部緊、可分、第一可數、連通、道路連通、局部連通、局部道路連通空間.[1] ...
當X=Rn時,X上的通常拓撲滿足一切分離公理,是σ緊、林德勒夫、局部緊、可分、第一可數、第二可數、仿緊、亞緊、全體正規、連通、道路連通、局部連通空間。但不...
