每個對稱運算元都有閉的對稱擴張。如果對稱運算元T沒有真的對稱擴張,即若T⊂S且S是對稱運算元一定有T=S成立時,則稱T是極大對稱的(maximally symmetric )。在一定條件下,對稱運算元與等距運算元可通過凱萊變換相互轉化。凱萊變換在對稱運算元和部分等距運算元之間建立了一種對應關係。
基本介紹
- 中文名:對稱運算元
- 外文名:symmetry operator
- 適用範圍:數理科學
定義介紹

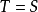
凱萊變換

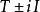






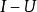


每個對稱運算元都有閉的對稱擴張。如果對稱運算元T沒有真的對稱擴張,即若T⊂S且S是對稱運算元一定有T=S成立時,則稱T是極大對稱的(maximally symmetric )。在一定條件下,對稱運算元與等距運算元可通過凱萊變換相互轉化。凱萊變換在對稱運算元和部分等距運算元之間建立了一種對應關係。

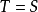

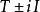






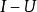

每個對稱運算元都有閉的對稱擴張。如果對稱運算元T沒有真的對稱擴張,即若T⊂S且S是對稱運算元一定有T=S成立時,則稱T是極大對稱的(maximally symmetric )。在一定...
對稱化運算元(symmetrization operator)是作用於反對稱張量上的運算元。張量是向量概念的綜合,可用以代表各向量間的關係。例如彈性張量把彈性體上每一點的變形與外加應力...
反對稱化運算元(anti-symmetrization operator)是作用於反對稱張量上的運算元。...... 反對稱化運算元(anti-symmetrization operator)是作用於反對稱張量上的運算元。...
在數學裡,作用於一個有限維的內積空間,一個自伴運算元(self-adjoint operator)等於自己的伴隨運算元;等價地說,表達自伴運算元的矩陣是埃爾米特矩陣。埃爾米特矩陣等於自己...
本質自伴運算元(essentially self-adjoint operator)具有自伴擴張的對稱運算元。...... 本質自伴運算元(essentially self-adjoint operator)具有自伴擴張的對稱運算元。...
對稱函式代數(symmetric functional algebra),是對稱代數的一個重要例子。...... 其中、為對稱運算元,則是一個可換的結合代數,稱為E的對稱函式代數.詞條標籤: 科學 ...
完全對稱化子(completely symmetrizer)是張量空間上的一種投影運算元,有時也稱為對稱化子。多重線性代數的重要概念。定義有張映射的一種向量空間。具體定義有多種不...
非線性運算元又稱非線性映射,不滿足線性條件的運算元。泛函分析的研究對象主要是線性運算元及其特殊情況線性泛函。但是,自然界和工程技術中出現的大量問題都是非線性的。...
《線性運算元譜理論及其套用》科學出版社2013-3出版。...... 《線性運算元譜理論及其套用》介紹線性運算元及其譜的基本概念,無界對稱運算元、J-對稱運算元和C-對稱運算元的擴張...
