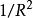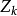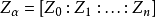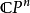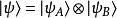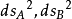構造
具體地,可以定義CPn由Cn+1中復直線組成的空間,即Cn+1在將一點與其所有複數倍聯繫在一起的等價關係下的商。這與在乘法群C*=C\ {0} 的對角群作用下的商相同:
這個商將
Cn+1實現為底空間
CPn上的複線叢(事實上這就是
CPn上所謂的重言叢)。
CPn中的一點等同於 (
n+1)-元組 [
Z0,...,
Zn] 模去非零復縮放的一個等價類;這些
Zi稱為這個點的
齊次坐標。
進一步,我們可以分兩步實現這個商:因為乘以一個非零複數
z=
R e可以惟一地想成一個以模長
R為因子的縮放與沿著原點一個逆時針旋轉角度
的複合,商
Cn+1→
CPn分成兩塊。
其中第 (a) 步以正實數乘法群
R+的縮放
Z~
RZ,這裡
R∈
R+,作商;步驟 (b) 是關於旋轉
Z~
ejθZ的商。第 (a) 步所得的商是由方程 |
Z|
2= |
Z0|
2 +...+|
Zn|
2=1 所定義的實超球面
S2n+1。第 (b) 步的商實現為
CPn=
S2n+1/
S1,這裡
S1表示旋轉群。這個商由著名的
霍普夫纖維化S1→
S2n+1→
CPn實現 ,纖維屬於
中的
大圓。
曲率性質
在
n= 1 的特例,富比尼–施圖迪度量具有恆等於 4 的
數量曲率,因為它與 2-球面的圓度量等價(半徑
R球面的數量曲率是
)。但是,對
n> 1,富比尼–施圖迪度量沒有常曲率。其
截面曲率由下列方程給出
這裡
是 2-維平面 σ 的一個標準正交基,
J:
TCPn→
TCPn是
CPn上的復結構,而
是富比尼–施圖迪度量。
富比尼–施圖迪度量經常稱為有等於 4 的常全純截面曲率。這使CPn成為一個(非嚴格的)四分之一拼擠流形(quarter pinched manifold);一個著名的定理指出嚴格四分之一拼擠單連通n-流形一定同胚於球面。富比尼–施圖迪度量也是一個愛因斯坦度量,它與里奇張量成比例:存在一個常數 λ 使得對所有i,j我們有
除此以外,這蘊含著,在差一個數量相乘的意義下,富比尼–施圖迪度量在里奇流下不變。這也使
CPn與廣義相對論不可分離,它是真空愛因斯坦方程的一個非平凡解。
量子力學
這裡
是
希爾伯特空間的一個正交規範基向量集合,
是複數,而
是射影空間
中一點在
齊次坐標中的標準記號。那么,給定空間中兩點
與
,它們之間的距離是
這裡
是
的復共軛。分母中出現的
提醒了
以及類似的
不是單位長規範化的;故這裡明確地做了一個規範化。在希爾伯特空間中,此度量可相當平凡地理解為兩個向量之間的角度;故它又稱為
量子角(quantum angle)。這個角度是實值的,取值於零到
。
通過取
,或等價地
,馬上可以等到這個度量的無窮小形式
在
量子力學中,
CP叫做
布洛赫球面;富比尼–施圖迪度量是量子力學幾何化的自然
度量。量子力學的許多獨特的行為,包括
量子糾纏和貝里相位(Berry phase)效應,可以歸於富比尼–施圖迪度量的特性。
乘積度量
通常的可分性概念適用於富比尼–施圖迪度量。更準確地講,此度量在射影空間的自然乘積
塞格雷嵌入(Segre embedding)中是可分的。這是說如果
是一個可分態,從而可以寫成
,則度量是子空間上度量之和:
相關條目
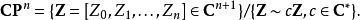
 的複合,商Cn+1→CPn分成兩塊。
的複合,商Cn+1→CPn分成兩塊。

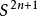
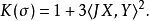


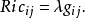




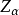




 ,或等價地
,或等價地 ,馬上可以等到這個度量的無窮小形式
,馬上可以等到這個度量的無窮小形式