完全統計量(complete statistic)亦稱完備統計量,是一類重要的統計量。由完全統計量的定義:E(g(S))=0對任意參數θ均成立時,即E=0對任意參數θ均成立,此時由T是完全統計量。
基本介紹
- 中文名:完全統計量
- 外文名:complete statistic
- 學科:數學,統計學
背景
定義

特徵
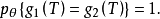

完全統計量(complete statistic)亦稱完備統計量,是一類重要的統計量。由完全統計量的定義:E(g(S))=0對任意參數θ均成立時,即E=0對任意參數θ均成立,此時由T是完全統計量。

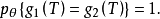
完全統計量(complete statistic)亦稱完備統計量,是一類重要的統計量。由完全統計量的定義:E(g(S))=0對任意參數θ均成立時,即E=0對任意參數θ均成立,此時由T...
完備統計量( complete statistic)數理統計概念。若存在一個統計量,使得對於總體參數的任意函式,基於該統計量的無偏估計至多只有一個,則稱之為完備統計量。 ...
有界完全統計量(boundedly complete statistic)是常用的一類完全統計量,設(X,BX,P)是一個統計結構,其中P={Pθ:θ∈Θ},如果對於BX可測的有界函式φ(X),由...
統計量是統計理論中用來對數據進行分析、檢驗的變數。巨觀量是大量微觀量的統計平均值,具有統計平均的意義,對於單個微觀粒子,巨觀量是沒有意義的.相對於微觀量的...
對於給定的統計推斷問題,包含了原樣本中關於該問題的全部有用信息的統計量。對於未知參數的估計問題,保留了原始樣本中關於未知參數θ的全部信息的統計量,就是充分...
在統計學中,一個統計量被稱完全的,或完備的,如果不存在由其構造的非平凡的0的無偏估計量(estimator)。在圖論中,一個圖被稱為完全的,如果這個圖是無向圖,...
請查看完全測度空間(complete measure)。 [4] 完備性統計學 編輯 在統計學中,一個統計量(statistic)被稱為完全的,如果它不允許存在0的無偏估計量(estimator)。...
U統計量(U-statistic)是一種重要的統計量,是霍夫丁(W.Hoeffding)於1948年引進的一種非參數統計量,是樣本均值的推廣。統計量(statistic)是指樣本的已知函式,其...
卡方統計量是指數據的分布與所選擇的預期或假設分布之間的差異的度量。在1900年由英國統計學家pearson提出,是用於卡方檢驗中的一個統計量。它可用於檢驗類別變數...
1.4 統計判決的基本概念 1.5 充分統計量 1.6 完全統計量 第二章 點估計 2.1 無偏估計 2.2 Cramer Rao型不等式 2.3 Bayes估計和Minimax估計 2.4 不變估計與...
“統計量關鍵字=自定義變數名”用來自定義輸出數據檔案中各種統計量的變數名稱,前者是系統定義的(和proc語句後選項中的統計量關鍵字完全相同),必須正確無誤,後者可...
由被估計參數的充分統計量構造出來的,包含了樣本(X1,X2……,Xn)中關於θ的全部信息的估計量。數學上,稱估計量為充分的,如果它是最小充分統計量的函式。 估計...
點估計(point estimation)是用樣本統計量來估計總體參數,因為樣本統計量為數軸上某一點值,估計的結果也以一個點的數值表示,所以稱為點估計。點估計和區間估計屬於...
