基本介紹
- 中文名:充分統計量
- 外文名:Sufficient statistics
- 所屬學科:統計學
- 相關概念:分布函式、密度函式、後驗分布等
- 提出者:費希爾
基本介紹
定義與判斷
定義







定理




統計量的判斷
在貝葉斯統計中判斷一個統計量是充分統計量也有一個充要條件。
定理
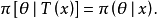


注意點
2.如果已知統計量

例題解析














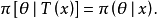





對於給定的統計推斷問題,包含了原樣本中關於該問題的全部有用信息的統計量。對於未知參數的估計問題,保留了原始樣本中關於未知參數θ的全部信息的統計量,就是充分...
統計量是統計理論中用來對數據進行分析、檢驗的變數。巨觀量是大量微觀量的統計平均值,具有統計平均的意義,對於單個微觀粒子,巨觀量是沒有意義的.相對於微觀量的...
由被估計參數的充分統計量構造出來的,包含了樣本(X1,X2……,Xn)中關於θ的全部信息的估計量。數學上,稱估計量為充分的,如果它是最小充分統計量的函式。 估計...
設X1,X2, …, Xn是取自總體X的樣本,X(i) 稱為該樣本的第i個次序統計量,它的取值是將樣本觀測值由小到大排列後得到的第i個觀測值。從小到大排序為x(1...
1.4 統計判決的基本概念 1.5 充分統計量 1.6 完全統計量 第二章 點估計 2.1 無偏估計 2.2 Cramer Rao型不等式 2.3 Bayes估計和Minimax估計 2.4 不變估計與...
《高等數理統計》是2007年北京大學出版社出版的圖書。[1] 本書主要介紹了現代...4.2 充分統計量4.3 完備統計量4.4 機率密度函式中的指數型分布族...
《充分統計量方法在醫療保障水平最佳化設計中的套用探索》,71303167,國家自然科學基金項目,2014/01-2016/12,已結題,主研。《經濟政策對居民消費、資產選擇及財富分配...
[41] 侯代文,殷福亮,陳喆,基於充分統計量的粒子濾波方法,信息與控制,2009,38(2), 187-193[42] 張麗艷,殷福亮,李細林,基於語音建立信號的ROTH加權時延估計方法...
點估計(point estimation)是用樣本統計量來估計總體參數,因為樣本統計量為數軸上某一點值,估計的結果也以一個點的數值表示,所以稱為點估計。點估計和區間估計屬於...
充分性與完備性 1.5.1 統計量的壓縮數據功能 1.5.2 充分統計量 1.5.3 因子分解定理 1.5.4 最小充分統計量 1.5.5 分布族的完備性 1.5.6 完備統計量 1.5....
