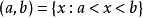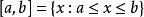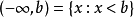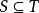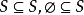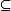孤立元素

對於一個集合A，當x∈A時，若有x-1不∈A，並且x+1不∈A，則稱x為A的一個孤立元素。

基本介紹

• 中文名：孤立元素
• 領域 ：數學
• 學科：集合論
• 對象：集合
• 性質：元素

概念

對於一個集合A，當x∈A時，若有x-1不∈A，並且x+1不∈A，則稱x為A的一個孤立元素。例如集合S={1,2,3,5,7}，5和7是孤立元素，因為4，6，8不屬於集合S或集合B={5,7,9,10}，5和7是孤立元素，因為4，6，8不屬於集合B。

集合

集合（簡稱集）是數學中一個基本概念，它是集合論的研究對象，集合論的基本理論直到19世紀才被創立。最簡單的說法，即是在最原始的集合論——樸素集合論中的定義，集合就是“確定的一堆東西”。集合里的“東西”，叫作元素。

由一個或多個確定的元素所構成的整體叫做集合。若x是集合A的元素，則記作x∈A。集合中的元素有三個特徵：1.確定性（集合中的元素必須是確定的）。 2.互異性（集合中的元素互不相同）。例如：集合A={1，a}，則a不能等於1）。 3.無序性（集合中的元素沒有先後之分），如集合{3,4,5}和{3,5,4}算作同一個集合。

元素

集合是指具有某種特定性質的具體的或抽象的對象匯總成的集體，這些對象稱為該集合的元素。

例如全中國人的集合，它的元素就是每一個中國人。我們通常用大寫字母如A,B,S,T,...表示集合，而用小寫字母如a,b,x,y,...表示集合的元素。若x是集合S的元素，則稱x屬於S，記為x∈S。若y不是集合S的元素，則稱y不屬於S，記為y∉S。一般的我們把含有有限個元素的集合叫做有限集，含無限個元素的集合叫做無限集。

集合分類

空集

有一類特殊的集合，它不包含任何元素，如{x|x∈R x²+1=0} ，我們稱之為空集，記為∅。

空集是個特殊的集合，它有2個特點：

1. 空集∅是任意一個非空集合的真子集。
2. 空集是任何一個集合的子集。

子集

設S，T是兩個集合，如果S的所有元素都屬於T ，即則稱S是T的子集，記為。顯然，對任何集合S ，都有。其中，符號讀作包含於，表示該符號左邊的集合中的元素全部是該符號右邊集合的元素。

如果S是T的一個子集，即，但在T中存在一個元素x不屬於S ，即，則稱S是T的一個真子集。

相等

如果兩個集合S和T的元素完全相同，則稱S與T兩個集合相等，記為S=T 。顯然我們有

其中符號稱為若且唯若，表示左邊的命題與右邊的命題相互蘊含，即兩個命題等價。

並交集

並集定義：由所有屬於集合A或屬於集合B的元素所組成的集合，記作A∪B（或B∪A），讀作“A並B”（或“B並A”），即A∪B={x|x∈A,或x∈B}。並集越並越多。

交集定義：由屬於A且屬於B的相同元素組成的集合，記作A∩B（或B∩A），讀作“A交B”（或“B交A”），即A∩B={x|x∈A,且x∈B}。交集越交越少。

若A包含B，則A∩B=B，A∪B=A。

補集

相對補集定義：由屬於A而不屬於B的元素組成的集合，稱為B關於A的相對補集，記作A-B或A\B，即A-B={x|x∈A，且x∉B'}。

絕對補集定義：A關於全集合U的相對補集稱作A的絕對補集，記作A'或∁u（A）或~A。有U'=Φ；Φ'=U。

冪集

定義：設有集合A，由集合A所有子集組成的集合，稱為集合A的冪集。

定理：有限集A的冪集的基數等於2的有限集A的基數次冪。

區間

數學分析中，最常遇到的實數集的子集是區間。

設a，b(a<b)是兩個相異的實數，則滿足不等式a<x<b的所有實數x的集合稱為以a，b為端點的開區間，記為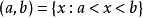；滿足不等式的所有實數的集合稱為以a，b為端點的閉區間，記為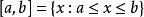；滿足不等式或的所有實數x的集合稱為以a，b為端點的半開半閉區間，分別記為及。除此之外，還有下述幾類無限區間：