基本介紹
- 中文名:門格海綿
- 外文名:Menger Sponge
- 分類:分形幾何學
定義,結構,性質,正式定義,參見,
定義
門格海綿是分形的一種。它是一個通用曲線,因為它的拓撲維數為一,且任何其它曲線或圖都與門格海綿的某個子集同胚。它有時稱為門格-謝爾賓斯基海綿或謝爾賓斯基海綿。它是康托爾集和謝爾賓斯基地毯在三維空間的推廣。
結構
門格海綿的結構可以用以下方法形象化:
- 從一個正方體開始。(第一個圖像)
- 把正方體的每一個面分成9個正方形。這將把正方體分成27個小正方體,像魔方一樣。
- 把每一面的中間的正方體去掉,把最中心的正方體也去掉,留下20個正方體(第二個圖像)。
- 把每一個留下的小正方體都重複第1-3個步驟。
把以上的步驟重複無窮多次以後,得到的圖形就是門格海綿。
性質
門格海綿的豪斯多夫維為(ln 20) / (ln 3)(大約2.726833)。
門格海綿的表面積無窮大。
正式定義
正式地,門格海綿可以定義如下:
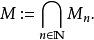
其中M0是單位立方體,且:


