一般認為當土中孔隙體積的80%以上為水充滿時,土中雖然有少量氣體存在,但大都是封閉氣體,就可視為飽和土。為求飽和土層在滲透固結過程中任意時間的變形,通常採用太沙基(K.Terzaghi,1925)提出的一維固結理論進行計算。
基本介紹
- 中文名:太沙基一維固結理論
- 外文名:Terzaghi's one-dimensional consolidation theory
- 學科:土力學
- 用途:求飽和土層在滲透固結過程中變形
基本假設
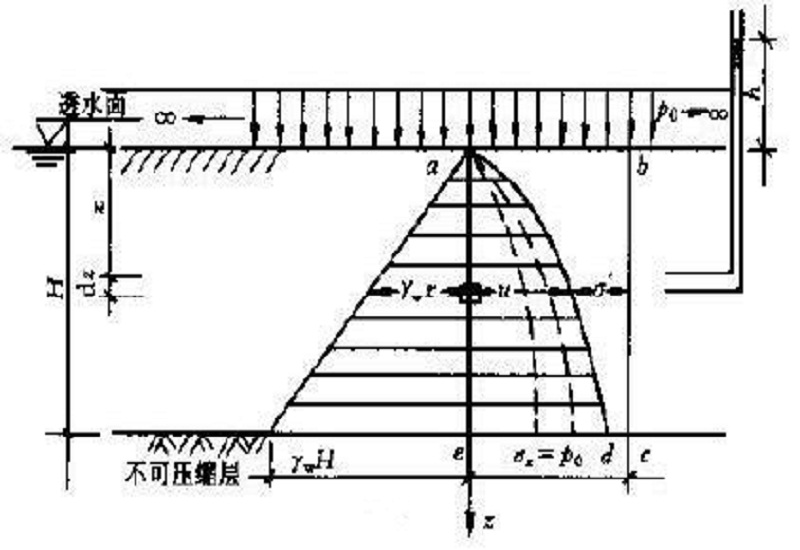
 圖1
圖1微分方程
方程建立
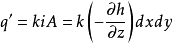
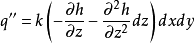
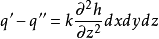
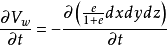
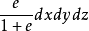
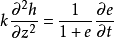
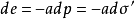
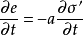
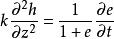
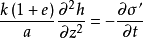
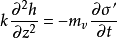
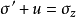
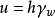
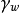
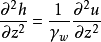
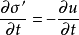
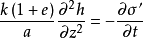
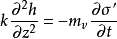
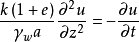
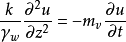
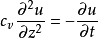
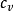
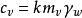
方程解析解
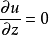
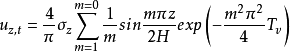
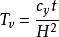
一般認為當土中孔隙體積的80%以上為水充滿時,土中雖然有少量氣體存在,但大都是封閉氣體,就可視為飽和土。為求飽和土層在滲透固結過程中任意時間的變形,通常採用太沙基(K.Terzaghi,1925)提出的一維固結理論進行計算。
 圖1
圖1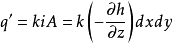
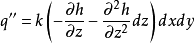
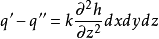
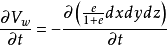
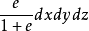
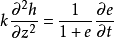
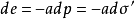
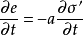
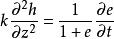
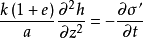
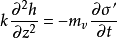
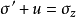
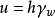
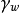
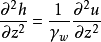
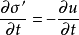
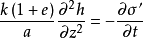
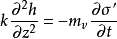
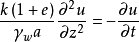
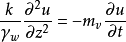
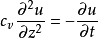
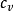
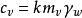
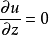
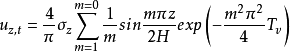
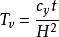
太沙基固結理論是指太沙基在1924年建立的一維固結模型和建立了一維固結理論。太沙基一維固結理論為求飽和土層在滲透固結過程中任意時間的變形,通常採用太沙基提出...
太沙基一維固結理論編輯 鎖定 一般認為當土中孔隙體積的80%以上為水充滿時,土中雖然有少量氣體存在,但大都是封閉氣體,就可視為飽和土。為求飽和土層在滲透固結...
太沙基在1924年建立了一個一維固結模型和建立了一維固結理論。太沙基一維固結理論為求飽和土層在滲透固結過程中任意時間的變形,通常採用太沙基提出的一維固結理論...
太沙基固結理論只在一維情況下是精確地,對二維、三維問題並不精確。比奧(Biot)從較嚴格的固結機理出發推導了準確反映孔隙壓力消散與土骨架變形相互關係的三維固結...
研究土體材料固結特性的理論基礎是Terzaghi(太沙基)的飽和土一維固結理論[1] 。土體固結分類 編輯 飽和土的固結; 非飽和土的固結; 靜力固結; 動力固結。 ...
太沙基-倫杜列克擴散方程,又稱太沙基-倫杜列克固結理論,該理論與太沙基一維固結理論建立在同一個理論基礎上,即在飽和粘土的固結過程中,土中任意單元體的體積...
研究這兩種應力的相互消長以及土體變形達到最終值的過程,稱為固結理論。1924年,太沙基提出一維固結理論和有效應力原理,建立了土體的一維固結理論,奠定了現代土力學的...
5.5土體的固結理論………(175)5.5.1太沙基一維固結理論………(176)5.5.2荷載隨時間變化時的固結計算………(182)5.5.3固結係數的試驗...
太沙基固結理論只在一維情況下是精確地,對二維、三維問題並不精確。比奧(Biot)從較嚴格的固結機理出發推導了準確反映孔隙壓力消散與土骨架變形相互關係的三維固結...
5.4.2 太沙基一維固結方程及其解 5.4.3 初始超靜孔壓非均布時的一維固結解 5.4.4 一維固結理論的套用 習題與思考題 參考文獻 第6章 地基沉降計算 6...
4.4.1太沙基一維滲流固結理論153 4.4.2關於滲流固結理論的研究進展162 習題164第5章土的抗剪強度168 5.1概述168 5.2土的抗剪強度理論169 5.2.1直剪試驗與...
土的壓縮性與地基沉降計算,土的抗剪強度理論,土壓力計算,土坡穩定分析和地基...4.4.1飽和土的滲流固結模型 1404.4.2太沙基一維滲流固結理論 142...
土層的排水固結效果與其排水邊界有關,根據太沙基一維固結理論,土層固結所需時間與排水距離的平方成正比,因此可用增加土層的排水途徑、縮短排水距離的辦法來加速土層的...
第4章 軟土的固結與流變特性 4.1 固結基本理論 4.1.1 太沙基一維固結理論 4.1.2 比奧固結理論 4.2 雙層地基固結理論 4.2.1 雙層地基的定義 4.2.2 攪拌樁處...
4.5.1太沙基一維固結理論 4.5.2固結微分方程求解 4.5.3固結度 4.5.4用實測沉降推算後期沉降 本章小結 思考題 習題 第5章土的抗剪強度 5.1概述 5.2土的抗...
土的固結理論 第一節 一維固結理論 第二節 太沙基三維固結理論 第三節 比奧固結理論 第四節 非飽和土固結 參考文獻第八章 土體的流變理論 第一節 土體的流...
自從太沙基(K. Terzaghi)的一維固結理論問世以來,地基的沉降理論研究已經取得了長足的進步,並且在工程建設中發揮了巨大的指導作用。然而,從工程建設的發展與要求...
固結係數Cv 是太沙基( Terzaghi)一維固結理論中的一個重要參數,與固結過程中的超靜孔隙水壓力(u)的消散速率 成正比,其大小反映軟土固結快慢的程度,即固結係數為...
