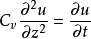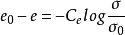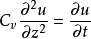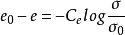太沙基固結理論是指太沙基在1924年建立的一維固結模型和建立了一維固結理論。太沙基一維固結理論為求飽和土層在滲透固結過程中任意時間的變形，通常採用太沙基提出的一維固結理論進行計算。
基本介紹
- 中文名：太沙基固結理論
- 外文名：Terzaghi consolidation theory
- 提出人：太沙基
- 提出時間：1925年
- 假設：土是飽和的、均質的等
- 發展：Biot固結理論
簡介,基本假設及理論方程,理論研究,局限性,理論發展,
簡介
天然土體一般由三相組成，即礦物顆粒構成骨架，土骨架空隙內充填水和空氣。土體受到外力後，可以認為土體變形是孔隙中流體體積變化的結果。土體在外加荷載作用下，由於孔隙比減少而壓密變形，同時提高了強度。對於飽和土，只有當孔隙水擠出以後，變形才能產生。開始時，土中應力全部由孔隙水承擔。隨著孔隙水的擠出，孔隙水壓力逐步轉變為由土骨架承受的有效應力。研究這兩種應力的相互消長以及土體變形達到最終值的過程，稱為固結理論。
地基土的壓縮是由於孔隙水壓力減小，有效應力增大的結果。附加應力一定的條件下，求得某一時刻孔隙水壓力即可確定有效應力。地基的這種固結過程中，任意時刻的沉降變形量與最終沉降變形量的比值，即定義固結度。
一維固結又稱單向固結，是指土體在荷載作用下產生的變形與孔隙水的流動僅發生在一個方向上的固結。嚴格的一維固結只發生在室內有側限的固結試驗中，在實際工程中並不存在；但是在大面積均布荷載作用下的固結，可以近似為一維問題。
太沙基在1924年建立了一個一維固結模型和建立了一維固結理論。太沙基一維固結理論為求飽和土層在滲透固結過程中任意時間的變形，通常採用太沙基提出的一維固結理論進行計算。
基本假設及理論方程
太沙基固結理論採用的物理模型的基本假設如下：
（1）土體是飽和的；
（2）土體是均質的；
（3）土顆粒和孔隙水在固結過程中都是不可壓縮的；
（4）土中水的滲流服從於達西定律；
（5）在固結過程中，土的滲透係數k是常數；
（6）在固結過程中，土的壓縮係數a是常數；
（7）外部荷載是一次瞬時施加的；
（8）土體的固結都是小變形；
（9）土中水的滲流與土體變形只發生在一個方向。
土中附加應力沿水平面是無限均勻分布的，因此土層的壓縮和土中水的滲流都是一維的；在這些假設的基礎上，太沙基建立了一維固結理論。許多的心的固結理論是在減少這些假設條件的基礎上發展起來的。所以說太沙基一維固結理論是最基礎有意義的固結理論。
對於均值地基，即使附加應力隨深度變化，但不同深度的同一水平面上的附加應力相同，則該水平面各個點的壓縮變形相同，且符合側限變性條件。當壓縮模量或壓縮係數不變時，對於任一隨深度變化的附加應力作用下，其單向固結變形可以套用疊加原理，相當於壓縮應力圖形中各部分在同一時刻引起變形的代數和。
根據上述基本假設最後推導得出的一維固結基本微分方程如下：
u—超靜孔壓；
Cv—固結係數。
理論研究
土的應力應變關係性狀是土力學的主要研究課題之一。由於土是一種複雜的工程材料其應力應變關係受許多因素影響，因而不可能期望在近期內提出一種普遍的應力應變關係，來描述各種不同類型的土在複雜加荷條件下的性狀。
在岩土工程計算中，大多還採用線性的、分段線性的或非線性的彈性應力應變關係。在 60 年代初期，英國劍橋大學提出了可以將正常固結粘土和輕度超固結粘土模擬為一種應變硬化的彈塑性材料，並且用增量塑性理論的方法研究土的應力應變關係。其它提出的彈塑性模型還有“拉德模型”、“雙屈服面模型”等。研究成果表明，彈塑性理論是研究土的應力應變關係的一個有力的數學工具，用它可以得出比較令人滿意的結果。
雖然國內外在土的應力應變關係研究方面有了不少新的進展，但在土的一維固結方面，工程實踐中仍延。用根據線彈性應力應變關係推導出的經典太沙基固結理論。實踐表明，如果仍然用經典的太沙基固結理論來解決一維固結問題，就會產生較大的誤差。這也是在軟粘土地區用太沙基固結理論求沉降時計算值與實測值差距較大的一個重要原因。要想在軟粘土分布地區比較精確地求解一維固結問題，其中一個重要的方法就是對經典的太沙基固結理論進行非線性應力應變關係方面的修正。Davis 和 Raymand 等在對經典的太沙基固結理論進行修正時，已採用較為實際的非線性應力應變關係——半對數型應力應變關係，即把孔隙比表示為有效應力對數的函式，如下式所示：
南京水利科學研究院魏汝龍教授通過大量試驗指出，軟粘土壓縮曲線的整個形狀更符合雙曲線的特徵，而不是半對數曲線。福州大學徐少曼也指出，在側限條件下，土的垂直壓力 P 和垂直側限應變ε的關係，可以用雙曲線良好地擬合。以壓縮試驗為基礎，用雙曲線來模擬土體的應力應變關係以及研究土體的固結特性。
經過學者的試驗研究，太沙基理論孔壓計算結果明顯高於實測值，表現為計算的孔壓消散比實際的要慢。這是因為太沙基理論是建立在諸多假設基礎之上的，而這些假設是對實際情況的簡化，從而造成了理論計算結果與實測值的不符。其中有三個假設對太沙基理論計算結果的誤差影響較大：
( a) 太沙基固結理論假設固結係數為常數，並且是由常規壓縮試驗得來的； ( b) 太沙基理論假設飽和粘土是線彈性的； ( c) 太沙基理論假設固結過程中各點應變是相同的。
這明顯不符合實際，因為靠近排水面孔壓消散快，固結沉降進展也較快，所以應變數較大。相反，不排水面附近應變數則較小。雙曲線修正一維固結理論計算結果在加荷初始時，與太沙基理論結果相近，同樣偏高於實測值，但當孔壓消散波及到底部不排水面後，其結果就較好地反映了實際的孔壓消散過程。這表明，用雙曲線型應力應變關係對太沙基固結理論進行修正後，能夠較好地預測一維固結過程中孔壓的消散情況。通過本文的試驗驗證，說明了用雙曲線修正固結理論計算孔壓與太沙基理論相比同樣方便簡單，卻具有較高的精確性。從考慮土體非線性問題入手，根據太沙基固結問題的基本假設，做了一些修正，導出了雙曲線條件下的固結問題及其解，與室內試驗結果進行了對比。雖然提出的修正方法使計算結果更接近於試驗結果，但有關固結理論的研究還需要做更深入細緻的工作。
所以，綜上所述，經過不斷的努力和探索，基於一維太沙基固結理論的研究和發展，固結理論逐步的趨於完善，固結理論對於不同情形也有了很大的突破，但是固結理論的新的發展和套用還有待學者們的繼續研究和努力，希望能在岩土工程領域會有更大的突破和進展。
局限性
自太沙基一維固結理論提出的半個多世紀以來，人們已有大量的工程實踐和改進方法，但是問題仍然沒有完全解決。在實際工作中常常發現太沙基一維固結理論計算的沉降速率遠小於實測值。為此，設計人員常常感到困惑，選用勘探取樣室內試驗結果得到的壓縮性指標，進而求得固結計算結果到底有多大的把握。
傳統的固結理論(太沙基1923；太沙基 and Frolich1936) 是在岩土工程中套用範圍最廣的理論之一。這是因為它體現了固結的基本物理過程，採用的參數可由常規的室內試驗提供，而且可以手算求得計算結果。但是太沙基一維固結理論也存在著諸多不足之處。眾多學者針對固結度理論值與實際值相差過大，已從以下幾方面展開了大量的研究工作：
（1）魏汝龍寫道：軟粘土地基上的現場觀察資料表明，實際的沉降速率通常比用太沙基一維固結理論計算的快得多。顯然，許多實際工程都是在三維或二維條件下發生固結和變形的。太沙基一維固結理論中沒有計入水平向的孔隙壓力消散必然會加速其沉降速率。
太沙基與 Redulic 提出了準三維固結理論，其中包含三維的水流，但是只計入一維的豎向應變。此時就可象一維固結理論中那樣假設土中的總應力分布在固結過程中不變，從而可將孔壓的消散和豎向應變分開處理，簡化問題的求解，但總應力在固結過程中不變的假設使多維問題不能滿足彈性力學相容方程，所以太沙基- Redulic 三維固結理論是在多維問題中是不嚴格的。
比奧( Biot) 從較嚴格的固結機理出發，提出的固結理論可反映孔隙壓力消散與土骨架變形相互關係比太沙基固結理論及合理地反映土體的固結過程。但比奧固結理論的設計參數較多，由於岩土材料的複雜性，準確確定這些參數又比較困難；此外，按比奧方程求解固結問題的精確解是相當複雜的，目前所見的比奧解析解也只是在若干特殊情況下求得的。因此，通常須用有限元等數值方法求解，計算比較複雜，計算結果是否合理在很大程度上依賴於計算參數的取值，這些都限制了比奧固結理論在工程上的套用。
太沙基固結理論的重大局限在於假定固結過程中土體的總應力分布不變，荷載不可能瞬時施加。實際情況是往往具有一定的加荷歷史，固結過程中土體的應力分布在不斷變化。比奧（1941）基於微單元體的力的平衡條件和滲流連續原理建立了完善的固結理論。可見，比奧特固結理論，建立了孔隙水壓力、滲流、體變與有效應力之間的內在聯繫。即附加荷載作用產生孔隙水壓力；水力剃度作用產生滲流，引起孔壓消散和擴散；滲流產生體積變化，與有效應力變化引起土骨架體變一致。反之，土骨架體變引起有效應力變化；有效應力變化導致總應力與孔壓變化；孔壓變化促使滲流產生，使得滲流體變與土骨架體變一致；總應力變化與附加荷載作用效應等效。
（2）對於深厚軟土地基或超軟土地基，在較大的外載下，固結應變可達到 40%以上。這時太沙基一維固結理論的小應變假定就不合適了，需要大變形固結理論來分析。一維大變形固結理論始於 1960 年，Mikasa 和 Gibson被認為是這一領域的開拓者，他們都致力於把小變形固結理論推廣到更普遍的大變形固結理論。該理論認為壓縮係數不為常數，即有效應力與孔隙比之間有非線性關係；滲透係數與孔隙比有關；滲透速度以孔隙水與骨架的相對速度表示。它採用孔隙比e為控制變數，同時採用拉格朗日坐標或固相物質坐標，從而推求出基本方程。大變形固結理論沿著兩個方向發展，一方面，基於 Mikasa 和 Gibson 等人的理論，進行理論的完善和數值求解及試驗驗證；另一方面，隨非線性連續介質力學的發展，建立在其基礎之上的有限元分析也不斷取得進展。Olson和Ladd指出，一維固結微分方程進行差分求解時，如果考慮土層厚度的變化就可以自動處理大變形固結問題。
（3）天然地基往往都是水平成層狀地基，太沙基一維固結理論不能直接套用。Gray 早在 1945年即給出一維固結成層地基在瞬時加荷條件下的解析解。Home 和 Schiffman 以及 Stein 試圖通過引申經典的太沙基固結理論來模擬成層體系。謝康和求解出變荷載下任意層地基一維固結問題完整的解析解，從而使成層地基固結理論趨於完善。但是這些解析解很複雜，因此在實際設計中很少採用。計算成層地基平均固結度 U現有簡化方法有加權固結係數法和平均指標法。
（4）魏汝龍認為太沙基一維固結理論與觀察到的試驗事實不相符。他指出的兩個最重要的偏差之一是：當孔隙壓力消散到零時，沉降並不終止，隨之而來的一般是在常有效應力下的次壓縮或蠕動變形。這種土體體積的變化則稱為次固結現象。1965年 ASTM 標準中次固結的定義是：由於對土體施加持續時間很長的常荷重而引起的，並且主要是由於大部分荷重從土中水轉移到土骨架後，土體內部結構調整而產生的體積減小。最早的次固結理論是由 Taylor 和 Merchant( 1940) 提出來的。後來，陳宗基(1957) ，McNabb(1960)等又作出重要貢獻。這些理論方法的缺點主要在於難以試驗測定計算所需的參數，這就限制了它們的實際套用。Biot(1956) ，Mande( 1957) 和陳宗基( 1957) 提出的三維理論則更為複雜。Gibson和Lo(1961)，Bardon( 1965) ，Poskitt(1971)以及Garlanger(1972)等都研究了次固結效應。
（5）太沙基一維固結理論的實際套用中，一般採用固結過程中整個土層厚度各處的垂直應變都一樣的簡化假設。太沙基和Frolich(1936)，以及 Janbu指出隨著應變分布形式的不同，固結沉降速率是不一樣的。而在許多工程中，應變實際的分布是不均勻的。應變隨附加應力沿深度方向衰減而減小。當存在硬殼層時，硬殼層處的應變較小，而硬殼層下粘土的應變會變得很大。Duncan 以位於洛杉機海灣4處不同厚度的粘土層為例，用這種簡化假設進行計算，得出的結果出現反常現象，由此他指出這種簡化假設的不合理性。
理論發展
荷載作用時土體中產生超孔隙水壓力，在排水條件下隨著時間發展土體中水被排出，超孔隙水壓力逐步消散，土體中有效應力逐步增大，直至超孔隙水壓力完全消散，這一過程稱為固結。土體在固結過程中，隨著土中水的排出，土體孔隙比減小，土體產生壓縮，體積變小，隨著有效應力逐步增大，土體抗剪強度得到提高。
土體的固結規律相當複雜，它不僅取決於土的類別和狀態，也隨土的邊界條件、排水條件和受荷方式等因素而異。飽和土體的一維固結理論是太沙基（1925）首先提出的。後來，Rendulic(1936)將太沙基的一維固結理論推廣到二維和三維情況，得到太沙基- Rendulic固結理論。這個理論除了保留太沙基一維固結理論的假定條件外，還假定在排水固結過程中，土中一點總應力之和保持不變，即未考慮應力與應變需要滿足的相容條件。Biot（1941）進一步研究了三向變形材料與孔隙壓力的相互作用，直接從彈性理論出發，確保土中應力和應變滿足相容條件，得到了比較完善的三維固結方程。太沙基和Biot的固結理論均是建立在無限小應變的前提下，對更一般的情況，Schiffa（1980）總結了前人的研究成果，提出了一個更為普遍的固結理論表達式，它不僅考慮了應力-應變的非線性關係、滲透性隨有效應力的變化，而且考慮了大應變的情況，Teraghi固結方程和Biot固結方程都是這一普遍關係式的特殊情況。另外，Barron（1948）在太沙基單向固結理論的基礎上，建立了軸對稱固結基本微分方程，並導出其解析解，在砂井地基設計中得到廣泛套用。
幾十年來，固結理論的發展，主要圍繞著以下幾個方面：
1. 隨著土體微觀結構性研究的發展，對土體本構模型進行修正，假設不同土體材料的模式，而得到不同的物理方程：(1)土骨架假設為彈性的〔各向同性與各向異性的)，塑性的，粘彈性的(線性與非線性以及它們的各種組合；（2）土中流體假設為不可壓縮的，線性粘滯體的，可壓縮的；（3）土骨架與流體間相互作用的不同考慮等。
2. 進一步針對不同的土體特性、土層分布、邊界條件、排水條件以及加荷方式等，對原有的太沙基固結方程、Biot固結方程進行修正並求解。
3. 在運用數學工具推導固結方程的解析解的同時，藉助各種數值計算方法對固結問題進行半解析或者數值研究。
