基數算術(cardinal arithmetic)指基數的算術運算,即加法,乘法和冪運算。由於自然數就是有窮基數,因此,在有窮情況下,基數運算等同於自然數的運算,但對於無窮基數,情況則很不相同。
基本介紹
- 中文名:基數算術
- 外文名:cardinal arithmetic
- 所屬學科:數學(集合論)
- 簡介:基數的算術運算
- 內容:基數加法,基數乘法和其冪運算等
基本介紹
基數加法
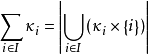
基數乘法
基數乘方運算
無窮基數的特殊性質




基數算術(cardinal arithmetic)指基數的算術運算,即加法,乘法和冪運算。由於自然數就是有窮基數,因此,在有窮情況下,基數運算等同於自然數的運算,但對於無窮基數,情況則很不相同。
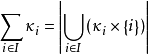



基數算術(cardinal arithmetic)指基數的算術運算,即加法,乘法和冪運算。由於自然數就是有窮基數,因此,在有窮情況下,基數運算等同於自然數的運算,但對於無窮基數,...
在數學上,基數(cardinal number)是集合論中刻畫任意集合大小的一個概念。兩個能夠建立元素間一一對應的集合稱為互相對等集合。例如3個人的集合和3匹馬的集合可以建立...
基數乘法(multiplication of cardinal numbers)是自然數乘法的超窮推廣,定義在基數類上的二元運算f:card²→card,若對任意的〈κ,λ〉∈card²,有f(κ,λ)=...
算術是數學中最古老、最基礎和最初等的部分,它研究數的性質及其運算。把數和數的性質、數和數之間的四則運算在套用過程中的經驗累積起來,並加以整理,就形成了最...
在數學上,基數(cardinal number)是集合論中刻畫任何集合大小的一個概念。兩個能夠建立元素間一一對應的集合稱為互相對等集合。例如3個人的集合和3匹馬的集合可以建立...
社會保險基數簡稱社保基數,是指職工在一個社保年度的社會保險繳費基數。它是按照職工上一年度1月至12月的所有工資性收入所得的月平均額來進行確定。社會保險繳費...
在集合論中,如果不能通過基數算術的通常操作從較小的基數中獲得不可數的基數,那么他就是不可達的。更準確地說,如果基數K不可數,那么他就是強烈不可達的,它不是...
養老金基數一般指“養老保險基數”,該基數指養老保險的繳費基數,是計算現在應當交納養老保險費比例的基數。這個基數主要與本人的工資基數有關,與未來的養老金數額、...
規費的計算基數...... 規費的計算基數 中文名 規費的計算基數 建安費用中有關規費的計算基數是根據:分部分項工程費+措施項目費中屬於計費的6項內容+其他項目費=計...
雙倍工資計算基數,也可稱雙倍工資計算標準、二倍工資計算基數、二倍工資計算標準,主要指我國勞動契約法第八十二條規定的“用人單位自用工之日起超過一個月不滿...
▪成都企業個人最新社保基數如下: 成都市社會保險徵收繳納比例一覽表 戶口基數類型險種繳費基數(元)單位繳費個人繳費合計執行時間 比例(%)金額(元)比例(%)金額(...
社保繳費基數是社會平均工資的60%--300%為繳納基數,比如社會平均工資是1000元,繳納的基數可以是600元--3000元。上海市 2004 年的情況為例, 2003 年社會月平均...
