基本介紹
- 中文名:圖解法
- 外文名:graphical method
- 所屬學科:數理科學
- 套用:求解線性規劃問題及其他數學運算
定義
線性規劃問題
解題步驟
例題解析
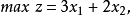

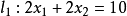
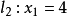
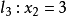
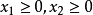
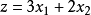
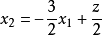
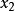
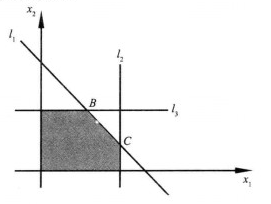 圖1
圖1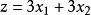
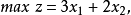

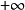
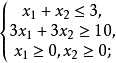
其他數學問題
適用範圍
例題解析
 圖2
圖2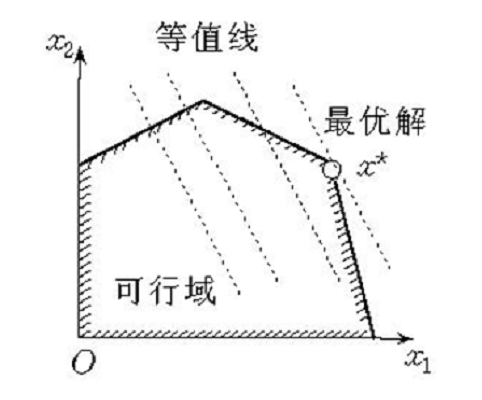
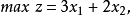

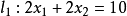
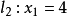
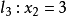
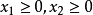
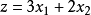
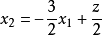
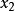
 圖1
圖1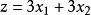
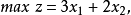

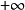
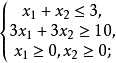
 圖2
圖2圖解法一般是指求解僅含兩個變數的線性規劃問題的一種方法。只含兩個變數的線性規劃問題,由約束條件確定的可行域可以在二維平面上表示出來,按照一定規則,在可行域...
圖解法測算面積是根據已有的房地產圖,採用各種不同的測量儀器量算出面積。包括求積儀法、稱重法、模片法、光電面積最算儀法等。...
線性規劃圖解法就是用幾何作圖的方法並求出其最優解的過程。求解的思路是:先將約束條件加以圖解,求得滿足約束條件的解的集合(即可行域),然後結合目標函式的要求...
歐拉圖解法又稱歐拉邏輯圖解法, 是一種邏輯學上的圖解,用來揭露兩個概念是否有重疊關係。...
《法華經》全稱《妙法蓮華經》,最大乘佛教中的一部重要經典,它是佛在入滅前所說,所以是最圓滿的佛法。無數僧俗都十分推崇《法華經》,認為它展示了廣大無邊...
圖解法放邊樁(sloe stake by diagram)是指將各樁號的路基橫斷面按比例繪在方格紙上,按圖定出中心樁至路塹邊坡頂或路堤坡腳的距離,在實地定出邊樁的方法。...
靜力圖解法 (graphic method of statics)又稱圖解靜力學(graphic statica),靜力學中用作圖方式求解同題的一種方法。...
放大器圖解法常見分析方法有:圖解法、估算法和等效電路分析法。...... 放大器圖解法常見分析方法有:圖解法、估算法和等效電路分析法。基本放大器的常見分析方法有:...
《框式圖解法與中學語文教學》除“前言”外,共安排六章:短語、單句、複句、句群、篇章、作文。我們認為,語法知識必須講,但要根據中學語文實際,大膽取捨,化簡、...
《心律失常梯型圖解法》是2006年浙江大學出版社出版的圖書,作者是吳祥。本書主要由總論、梯形圖解法及與心律失常相關的診斷技術三部分組成。...
2.3 線性規劃模型的圖解法 2.4 最小化模型舉例 2.5 不規則線性規劃問題 2.6 線性規則問題的特徵 小結 參考文獻 例題求解 習題 案例問題 第3章 線性規則:計算機...
角圖法(angle diagram)是指在既有線改建中,利用角圖面積計算既有曲線撥距的方法。是漸伸線的圖解法。前蘇聯20世紀40年代末開始使用。...
分析多重複句可以採用符號法和框式圖解法。如:(1).符號法:①有些人背上雖然沒有包袱,‖(並列)②有聯繫民眾的長處,|(轉折)③但是不善於思考,|‖(並列)④不...
簡捷法一般是指一種精餾過程設計計算的簡化方法。圖解法適於二元精餾的設計計算,具有簡易直觀的優點。對於多組分精餾,圖解法不再適用,而需要採用簡捷法進行設計。...
1.2 線性規劃問題的圖解法1.2.1 圖解法的步驟1.2.2 線性規劃問題求解的幾種可能結果1.3 線性規劃的基本性質1.3.1 線性規劃的基本概念...
有兩個層次的叫二重複句,有三個層次的叫三重複句,其餘依次類推。多重複句是由一重複句擴展而成的。分析多重複句可以採用符號法和框式圖解法。如:(1)符號法:...
