靜力圖解法

靜力圖解法 (graphic method of statics)又稱圖解靜力學(graphic statica)，靜力學中用作圖方式求解同題的一種方法。

基本介紹

• 中文名：靜力圖解法
• 外文名：graphic method of statics

定義

靜力圖解法 (graphic method of statics)又稱圖解靜力學(graphic statica)，靜力學中用作圖方式求解同題的一種方法。所得結果的精確度雖不如數解法，但能迅速得出一目了然的答案，故在一般工程結構的設計中也常採用。用此法進行設計，便於隨時調整原始數據和迅速找出計算過程中的錯誤，並可用以比較幾種設計方案的長處和短處。

要點

靜力圖解法的要點可用下例來說明：

設有如圖1所示的平面任意力系F₁、F₂、F₃，它們分別作用於A₁、A₂、A₃，求此力系合力的大小、方向和作用線位置。

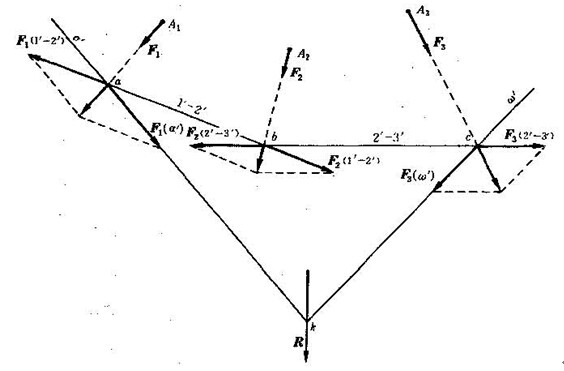
圖1 力系的索多邊形

先按比例作出表明各力相對大小和位置的力系圖，如圖1中的F₁、F₂、F₃再選一適當比例，作出此力系的力多邊形ABCD(圖2)，其封閉邊即為力系的合力R

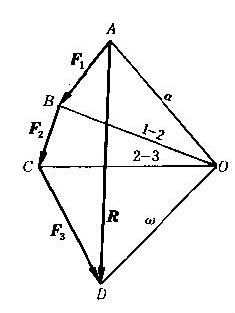
圖2 力系的力多邊形

在圖2中的邊多邊形近旁任選 一點O,O點稱為極點。用直線自O點連至多邊形的各個頂點A、B、C、D，這些直線稱為射線。射線OA、OB、OC、OD分別標記為α、1-2、2-3和ω。自圖1上的任意點作平行於力多邊形上α射線的直線α’，它與F₁的作用線交於α點；再自α點作平行於1-2射線的直線1’-2’，它與F₂的作用線交於b。照此進行，最後引直線ω’平行於射線ω，就行到一索多邊形abck，又稱伐里農多邊形。它的每一邊稱為索線。力系合力R的作用線必通過索線α’與ω’的交點k。

若力多邊形封閉，索多邊形的第一索線α'與最末索線ω'互相平行，則原力系合成為一力偶。若力多邊形封閉，索多邊形的第一索線α'與最末索線ω'重合，即索多邊形自行封閉，則原力係為平衡力系。因此，也可套用此法求解平衡力系的未知力。若為空間力系，則其基本畫法是以立體形狀繪成平面圖形的方法為依據，再作圖求解。由於方法較繁，一般不用。

套用這種圖解法也可求平面圖形的轉動慣量和重心，以及梁中的彎矩圖等。