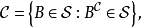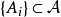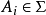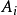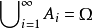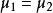基本介紹
- 中文名:單調類定理
- 外文名:monotone class theorem
- 所屬學科:數理科學
- 套用領域:測度論與機率論
- 相關定理:測度的唯一性定理等
定理介紹,證明過程,測度的唯一性定理,
定理介紹
證明過程
證明:設 是所有包含
是所有包含 的單調類的交,即
的單調類的交,即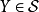 若且唯若Y屬於每個包含
若且唯若Y屬於每個包含 的單調類。我們留給讀者去驗證
的單調類。我們留給讀者去驗證 也是包含
也是包含 的單調類,從而由定義,它是這種單調類中最小的一個。
的單調類,從而由定義,它是這種單調類中最小的一個。


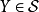



首先注意到只需證明 關於取余運算和有限並運算封閉,有了這兩個封閉性後,對
關於取余運算和有限並運算封閉,有了這兩個封閉性後,對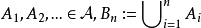 就是
就是 中一單調遞增集列,由於
中一單調遞增集列,由於 是單調類,
是單調類,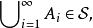 從而它關於可列並運算是封閉的。另外,從公式
從而它關於可列並運算是封閉的。另外,從公式

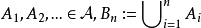


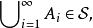








接下來證明 關於有限並是封閉的,固定集合
關於有限並是封閉的,固定集合 考查集族
考查集族 ,因為
,因為 是代數,所以
是代數,所以 )包含了
)包含了 ,再取
,再取 中任一遞增集列
中任一遞增集列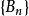 ,
, 顯然也是
顯然也是 中的遞增集列,由於
中的遞增集列,由於 是單調類,
是單調類,







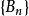





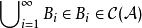



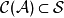



再取定 中任一元
中任一元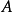 ,考查
,考查 ,從上段討論中得知
,從上段討論中得知 是
是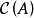 的子集,再對這個新的
的子集,再對這個新的 幾乎完全重複上一小段的討論,就會發現它也是單調類,從而有
幾乎完全重複上一小段的討論,就會發現它也是單調類,從而有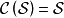 ,這樣就證明了
,這樣就證明了 關於有限並的封閉性。
關於有限並的封閉性。

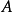


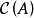

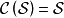

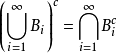


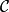
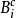

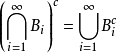



測度的唯一性定理
作為單調類定理的套用,我們敘述測度的唯一性定理,它闡明了套用單調類定理的一種典型方法。
測度的唯一性定理: