基本介紹
- 中文名:單種群模型
- 外文名:single-species models
- 所屬學科:生物數學
- 簡介:種群生態學的基礎模型
基本介紹
種群的幾何級數增長




(指數型增長)Malthus模型


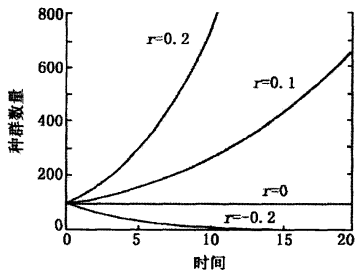
Logistic模型













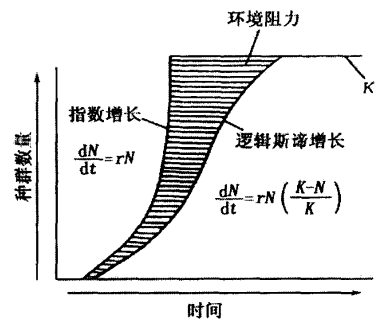
有收穫的單種群模型




具時滯的單種群模型





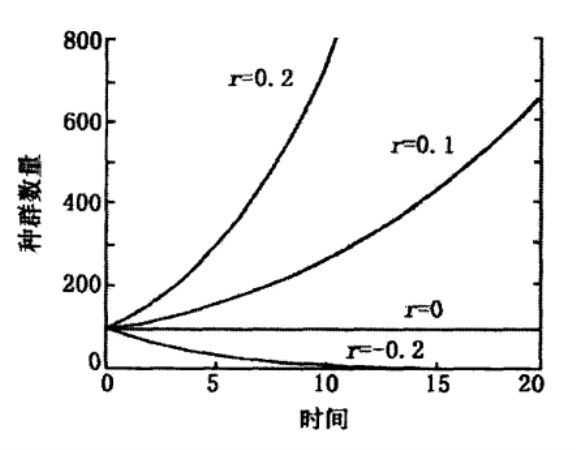






























單種群模型(single-species models)是種群生態學的基礎模型,指用以描述某一種群的密度(或個體數量)隨時間變化而改變的規律的數學模型。在自然界中,真正單一生存的種群是極少的,每一個種群在生物圈中必然屬於...
一般離散單種群模型(general single-speciesdiscrete model)一種常見的單種群模型.是離散單種群模型的一種更一般化的形式.若以x‘代表在時刻t種群的密度(或個體數量),則一般離散單種群模型可以寫為 其中(F<x)為非負連續函式(對所有x...
營養動力學種群模型(models of populationsbased on the nutrition kinetics)一種常見的單種群模型.指從生物生長依賴於環境中的營養物質供應這一基本概念出發建立的一種數學模型.該模型可表為 定義 x (t)為在時刻t的種群密度,x二為...
全書分為單種群模型、物種間相互作用模型、結構種群模型和疾病傳播模型4個部分,共10章.本書可作為生物學、醫學、數學等有關專業的大學本科生和研究生的教材,也可供種群生態學、傳染病學或進化論生物學等領域的科研人員參考使用.書中...
隨機生物模型主要介紹了基本的單種群模型、Lotka-Volterra型互惠和競爭模型以及具有不同功能反應函式的捕食-食餌模型在隨機擾動下正解的存在性、滅絕性、持久性和平穩分布的存在性等。隨機傳染病模型主要介紹了SIR傳染病模型在不同隨機擾動下...
5.2多種群時空離散模型 5.3病原生物體時空離散模型 第6章生物入侵的隨機模型 6.1單種群隨機模型 6.2多種群隨機模型 6.2.1捕食模型 6.2.2競爭模型 6.2.3其他模型 6.3病原生物體隨機模型 第7章生物入侵的精確解模型 7.1構造...
《種群生物結構模型與研究》是2010年科學出版社出版的圖書 內容簡介 《種群結構生物模型與研究》系統介紹了基本階段結構模型、複雜環境下的單種群階段結構模型、階段結構的種群競爭模型、資源—消費者系統、具有空間擴散的階段結構模型等方面的...
單種種群 單種種群,2006年公布的生態學名詞。
《微分方程建模與分析》是2014年科學出版社出版的圖書,作者是王春程、蘇 穎。內容簡介 全書共七章。內容包括:預備知識、單種群模型、捕食者-食餌模型、傳染病的倉室模型、化學反應模型建模分析 等。《微分方程建模與分析》可以作為高等...
不育控制是害鼠防治的新途徑,通過降低害鼠的生育率控制種群增長。本書涵蓋了國內外害鼠不育控制模型研究的主要成果,共分為7章:主要包括鼠類的基本特徵、不育控制機理及實驗研究進展、不育控制下的單種群模型、不育控制下的多種群...
第三節 數學生態模型 67 一、生態學模型的概念 68 二、建立生態模型的一般步驟 69 三、生態模型的一般成分 70 四、生態模型的類型 71 五、建立模型的一般方法 72 第四節 種群與種間關係模型 73 一、單種群模型 73 二、雙種群...
1.33人口模型(55)1.34單種群動物模型(59)1.35相對封閉環境中的傳染病模型(61)1.36江河污染物的降解係數(63)1.37怎樣計算固定資產的折舊(64)1.38放射性元素衰變模型(66)1.39市場上的商品價格是怎樣波動的(68)1.40再談下雪...
第4章 階段結構種群動力模型研究 4.1 引言 4.2 基本的階段結構模型 4.3 複雜環境下的單種群階段結構模型 4.4 階段結構的競爭系統 4.5 階段結構的捕食-食餌系統 4.6 階段結構種群模型未來可能的研究方向 第5章 恆化器模型研究...
