基本介紹
- 中文名:哈密頓圖
- 外文名:Hamiltonian graph
- 國家:美國
- 時間:1960年
- 學科:數學
- 套用:算法、路徑問題
哈密頓圈
判斷條件
算法級別


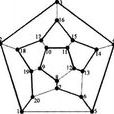


哈密頓通路(迴路)與哈密頓圖 (Hamilton圖) 通過圖G的每個結點一次,且僅一次的通路(迴路),就是哈密頓通路(迴路)。存在哈密頓迴路的圖就是哈密頓圖。美國圖論...
哈密頓圖(哈密爾頓圖)(英語:Hamiltonian graph,或Traceable graph)是一個無向圖,由天文學家哈密頓提出,由指定的起點前往指定的終點,途中經過所有其他節點且只經過...
哈密頓圈問題(Hamilton circuit problem)是圖論中著名的難題之一。巡迴售貨員問題有一個基於圖的天然類似問題,它是圖論中的一個基本問題,給定一個有向圖G(V,E)...
哈密頓(William Rowan Hamilton 1805~1865) 英國數學家,物理學家,力學家。1805年8月4日生於愛爾蘭都柏林;1865年9月2日卒於愛爾蘭都柏林。...
在磁場和電場理論中,為簡化運算,引入了一些運算元的符號,它們已經成為場論分析中不可缺少的工具,套用較多的有哈密頓運算元和拉普拉斯運算元。哈密頓運算元( Hamiltonian), ...
克里斯托弗·哈密頓圖,34歲,加拿大攝影師。 2016年,克里斯托弗·哈密頓圖進行海底冒險和探索,在索羅門群島發現二戰期間激戰被擊落的戰鬥機,在海底浸泡多年的戰鬥機...
哈密頓圈多面體(Hamiltonian circuit polytope)是一種特殊的多面體。它是由哈密頓圈導出的多面體。它的頂點相應一個圖上的哈密頓圈的鄰接矩陣。...
威廉·哈密頓爵士(Sir William Rowan Hamilton,1805年8月4日-1865年9月2日),愛爾蘭數學家、物理學家及天文學家。哈密頓最大的成就在於發現了四元數,並將之...
哈密頓原理,是英國數學家W.B.哈密頓1834年發表的動力學中一條適用於完整系統十分重要的變分原理。它可表述為:在N+1維空間(q1,q2,…,qN;t)中,任兩點之間...
量子力學中,哈密頓算符(Hamiltonian) H為一個可觀測量(observable),對應於系統的的總能量。一如其他所有算符,哈密頓算符的譜為測量系統總能時所有可能結果的集合...
哈密頓-凱萊定理(Hamilton-Cayley theorem)是矩陣的一個重要性質,該定理表述為:設A是數域P上的n階矩陣,f(λ)=|λE-A|=λn+b1λn-1+…+bn-1λ+bn是A...
介紹 哈密頓圈(Hamiltonian cycle)圖論術語.指 圖中包含所有頂點的圈一個圖若含有哈密頓圈,則 稱為哈密頓圖. ...
哈密頓力學是哈密頓於1833年建立的經典力學的重新表述,它由拉格朗日力學演變而來。拉格朗日力學是經典力學的另一表述,由拉格朗日於1788年建立。哈密頓力學與拉格朗日力學...
哈密頓量是一個物理辭彙,是系統的能量算符,是一個描述系統總能量的算符,以H表示。哈密頓量在大部分的量子理論公式中十分重要。...
在數學與物理中,哈密頓向量場是辛流形上一個向量場,定義在任何能量函式或哈密頓函式上。以物理學家和數學家威廉·盧雲·哈密頓命名。哈密頓向量場是經典力學中的...
經典力學中一組描寫系統運動的一階微分方程組。是W.R.哈密頓於1834年提出的,又稱哈密頓方程或正則方程。...
