基本介紹 設有一個圖,若其上存在一個圈,這個圈包含該圖上的每一節點,則稱該圈為哈密頓圈,這個圖稱為哈密頓圖.哈密頓圈問題可敘述為:什麼樣的圖為哈密頓圖,或者說判斷一個圖是哈密頓圖的行之有效的充分必要條件是什麼.目前這一問題尚未解決.關於哈密頓圈的研究,最早是歐拉(L.Euler)研究騎士(相當於中國象棋中的馬)從棋盤上的某一位置出發,走遍所有可能的位置且每個位置只通過一次後,回到原來的位置,而哈密頓(W.R.Hamilton)研究環遊世界的遊戲是在歐拉之後近一個世紀,然而卻由此開始引起人們對於這個問題的注意.實際上,哈密頓的遊戲就是,在一個正十二面體上,從一個頂點開始沿著棱走遍所有的十二個頂點回到原地,使得每一頂點只通過一次.就是在十二面體相應的圖上求一個哈密頓圈.若一個圖上存在一條路,這條路包含該圖上的所有節點,則稱該圖為可跡圖,稱這樣的路為哈密頓路,若對於一個圖上的每一節點,存在一個以該節點為始點的哈密頓路,則稱該圖為齊次可跡圖,一個圖被稱為哈密頓連通圖,若對於這圖上任何兩節點,存在一條哈密頓路連結這兩節點,稱一個圖為亞哈密頓圖,若從這圖上去掉無論哪一節點,所得的圖都是哈密頓圖,稱一個圖為亞可跡圖,若從這圖上去掉無論哪一節點,所得的圖都是可跡圖。
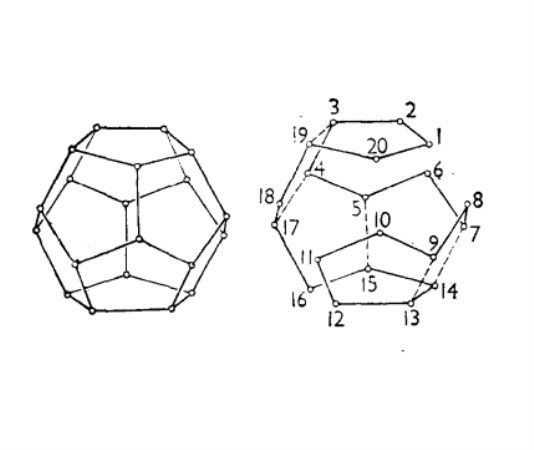
哈密頓圈 火星運河悖論 X國的人造火星衛星發現了火星上的運河水道還有20個城市遺址,如圖1所示。每個城市用一個拉丁字母來代表。最南邊的T是火星的“南極城”。X國《天地指南報》刊登了如下懸賞100萬美元征解的題目:從某個火星城出發,沿運河水路而行,每個城必須經過而且只經過一次,並且所經過的城市的代表字母恰好能拼寫成一句話。問,是否有這樣的途徑?如果有,請把它畫出來。
《天地指南報》編輯很快收到5萬多封讀者來信,都回答“不可能存在這樣的途徑”(There is no possible way)。
圖1 讀者的答案是“正確”的:圖1中已用1~20標出了這個途徑——從“南極城”T出發到達終點y。由一路上所經過的城市的代表字母,就拼寫成了“There is no possible way”,其含義是“不可能存在這樣的途徑”;但是,這句話的意思就是有這樣的途徑,即這樣的途徑是存在的。
從字面意思來看的話,“不可能存在這樣的途徑”(There is no possibleway)表示不存在題目中要求的途徑;而事實上又存在這樣的途徑。這就導致了自相矛盾的局面。這就是所謂的“火星運河悖論”。
讀者回答的“不可能存在這樣的途徑”,是這個圖1上的一條“哈密頓軌道”。如果從y再走到“南極城”T,則從“南極城”出發又回到了“南極城”,這又是一個“哈密頓圈”。這樣,圖1就是“哈密頓圖”。
為什麼都與哈密頓有關呢?
哈密頓週遊世界問題 1859年,英國數學家、物理學家威廉·羅恩·哈密頓(1805~1865),提出了以下“週遊世界遊戲”,據說公布在當地市場上:用圖2那樣的一個正12面體的20個頂點來表示地球上的20個城市,如何才能從某個城市出發,沿著各條棱走正好只經過每個城市一次,最後返回到出發地點?
圖2 圖3 哈密頓的問題,被他簡化為圖3的左或右所示的“棋盤”平面圖形問題。哈密頓還自豪地用棋盤做了形象明了的說明:“12面遨遊,單身周遊列國遊戲。
哈密頓 本玩具是欽命的愛爾蘭天文學博士、爵士威廉·羅恩·哈密頓的發明。宴席上,作為即興表演,稀奇無比。”
因為是皇帝欽命的天文學博士發明的玩具,大家都十分感興趣。於是,當時英倫三島掀起了一股“單身周遊列國”熱。
最後,這個問題已由哈密頓本人解決。他的答案如圖4所示,與前面的“不可能存在這樣的途徑”本質上相同。圖4中從1→20→1,就形成了一個哈密頓圈,即哈密頓圖。已經證明,除此之外採用別的本質不同的方式,是不能按要求週遊世界的。
圖4 不只外國人鐘情“單身周遊列國”,中國著名數學家蘇步青(1902-2003)也是“愛好者”之一。
蘇步青 蘇步青從圖3右邊“週遊世界棋盤”里的12個大大小小的五邊形中,挑出了6個(圖5中畫有斜線的那6個),這6個五邊形在原正12面體中的位置如圖6所示。再把圖6所示的6個五邊形“攤平”,就得到圖7那樣的有20個頂點的20邊形。
那么,到現在問題已經變得簡單化了。只要從圖7的點A出發,沿著20邊形的邊界走一圈,就可以“周遊列國”了。
哈密頓和蘇步青把一個12面體“壓扁”、變形後再進行研究的方法,值得我們深思。
“週遊世界棋盤”問題是哈密頓問題的特例,其對象後來也擴展為一般的m×n棋盤上走馬步的問題。用電子計算機研究之後,目前的成果有:對任意奇數的m,n,m×n,棋盤上不存在馬的哈密頓同路;西洋棋8 x 8的棋盤上至少存在10條哈密頓迴路;中國象棋9×10的棋盤上至少存在300條哈密頓迴路。這些問題,包括中國數學工作者在內的許多學者仍在不斷地尋找解決方法。
要判定一個圖是否具有哈密頓圈的問題,是圖論中著名的難題之一。除個別情形以外,迄今為止還沒有找到一個圖是否具有哈密頓圈的必要而且充分的條件。
哈密頓圈問題引出了諸如貨郎問題、郵遞員問題等類似的問題。比如,貨郎問題就是貨郎必須到每個村莊售貨,怎樣走才能使路程最短?當然,這個問題因為還要求“路程最短”,比哈密頓圈問題難度更大,以致用現代電子計算機來解決都很複雜。
這類問題的研究,促進了最最佳化方法、圖論等問題的研究,促進了運籌學、拓撲學等學科的發展。
 圖1
圖1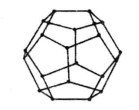 圖2
圖2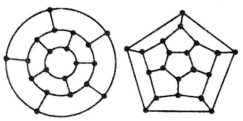 圖3
圖3 哈密頓
哈密頓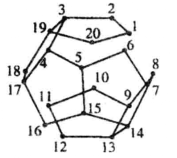 圖4
圖4 蘇步青
蘇步青