右平移是半群上的一類特殊變換。半群 S 上的一個變換 ρ(λ) ,若對任意x,y∈S,有 x(yρ)=(xy)ρ,(λx) y = λ(xy),則稱 ρ(λ) 為 S 的右(左)平移。
基本介紹
- 中文名:右平移
- 外文名:right translation
- 適用範圍:數理科學
半群中的右平移
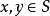
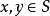


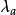
李群李代數中的右平移
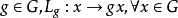
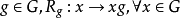



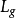


右平移是半群上的一類特殊變換。半群 S 上的一個變換 ρ(λ) ,若對任意x,y∈S,有 x(yρ)=(xy)ρ,(λx) y = λ(xy),則稱 ρ(λ) 為 S 的右(左)平移。
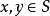
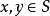


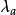
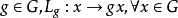
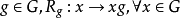



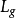

右平移是半群上的一類特殊變換。半群 S 上的一個變換 ρ(λ) ,若對任意x,y∈S,有 x(yρ)=(xy)ρ,(λx) y = λ(xy),則稱 ρ(λ) 為 S 的...
函式平移代表其在坐標系(或坐標平面)里的相對位置發生了變化,而對函式本身的性質和其代表的實際意義沒有任何影響。...
向左或向右平移拋物線時,可以簡記為“上加下減,左加右減”。因此,研究拋物線 y=ax2+bx+c(a≠0)的圖像,通過配方,將一般式化為y=a(x-h)2+k的形式,可...
結論:k<0時,圖象從左到右下降,y隨x的增大而減小。6.將函式向上平移n格,函式解析式為y=kx+b+n,將函式向下平移n格,函式解析式為y=kx+b-n,將函式向左...
1若把點A向左平移k(k>0)個單位後,坐標變為(x-k,y);若把點A向右平移k個單位後,坐標則變為(x+k,y).2.若把點A向上平移k(k>0)個單位後,坐標變為(...
斷層構造是岩層斷裂又其兩側發生相對運動的產物。按照斷層兩側岩塊相對運動的關係,它可以分為正斷層、逆斷層、右平移斷層、左平移斷層,又組合為正扭斷層、沖扭斷層...
L鍵 左平移 R鍵 右平移 Select鍵 乘坐作戰工具、救助倒地的同伴 Start鍵 開啟暫停選單 地球防衛軍3 攜帶版武器相關 編輯 地球...
右下方選單欄 17人物屬性:呼出人物屬性信息界面,可查看角色屬性、裝備等信息;18...向左轉:a 向左平移視角:left 向右轉:d 向右平移視角:right 向左走:q 向上...
使用該工具通過單擊及拖動來平移繪圖【H】按當前選項或工具顯示對象或工具的屬性...將鏡頭相對於繪畫右移【ALT】+【←】再制選定對象並以指定的距離偏移【Ctrl】+...
將文本對齊方式更改為右對齊【Ctrl】+【R】將文本插入記號向右移動一個字【Ctrl...將繪圖向上平移 【ALT】+【↑】將繪圖向下平移 【ALT】+【↓】...
A:左平移D:右平移滑鼠移動:查看四周滑鼠左鍵:射擊/放置方塊/挖方塊滑鼠右鍵:機械瞄準/放置方塊/挖方塊1,2,3,4切換武器(1:鏟子 2:方塊 3:武器 4:手雷)...
右 → 游標右移 右轉90度 / 右平移 確定 X / Enter 確認/ 選擇 前進一步 / 開門 取消 Z / Esc 取消/ 返回 紮營 副1 A 整理/ 開發 搜尋 副2...
將文本對齊方式更改為右對齊【Ctrl】+【R】將文本插入記號向右移動一個字【Ctrl...將繪圖向上平移 【ALT】+【↑】將繪圖向下平移 【ALT】+【↓】...
