如果存在一十狀態反饋“u=-Fx 使得閉環系統A+BF穩定,則稱系統(A,B)是可鎮定的。
基本介紹
- 中文名:可鎮定性
- 相關詞:可檢測性
簡介
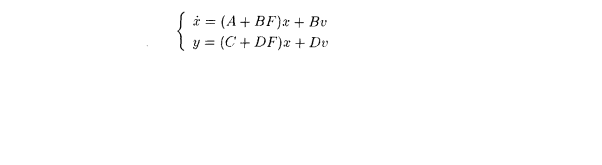
定義

例題

不完全能控系統的可鎮定性
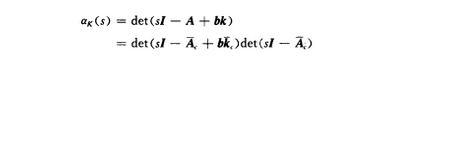

如果存在一十狀態反饋“u=-Fx 使得閉環系統A+BF穩定,則稱系統(A,B)是可鎮定的。
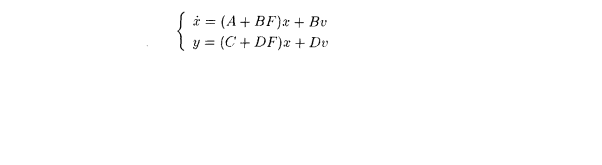



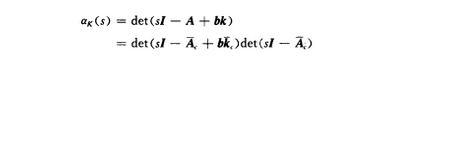
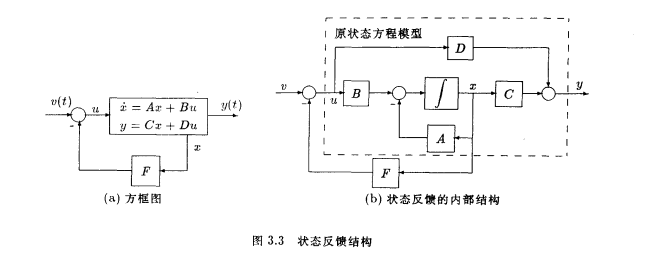
如果存在一十狀態反饋“u=-Fx 使得閉環系統A+BF穩定,則稱系統(A,B)是可鎮定的。簡介在介紹系統的可鎮定性和可檢測性之前,首先應介紹狀態反饋的概念,系統狀態反饋的示意圖如圖1左圖所示, 更詳細的內部結構如圖1右圖...
《多智慧型體系統的能控性與可鎮定性研究》是依託西安電子科技大學,由關永強擔任項目負責人的青年科學基金項目。中文摘要 多智慧型體系統的能控性與可鎮定性是近年來複雜智慧型系統研究中的熱點問題。現有的研究主要針對具有相同節點動力學的多智慧型體系統,且一般假設網路通信是無約束的。本項目研究具有通信約束和邊動力學的...
首先介紹可鎮定性的例子。狀態方程如下:其中矩陣對(Al1,C1)確定了一個能觀一維子系統。根據觀測器增益向量L=[Z.,Z。,l3]1,其中很容易選擇觀測器增益£,來單獨配置能觀子系統的特徵值。根據下三角矩陣塊結構, A-LC的三個特徵值為1+/1,和不能觀子系統的特徵值-1和-2。這樣可以得出結 論,雖然...
內容主要有:分數階控制系統的基礎知識,區間分數階系統的魯棒穩定性分析,區間分數階系統的分數階控制器可鎮定性,考慮穩定裕度時滯分數階系統的分數階PIA /PD控制器魯棒可鎮定域,不確定分數階系統的滑模控制,非線性分數階系統的自抗擾控制,分數階PI控制器用於永磁同步電機矢量控制系統的魯棒性。
6.2 有界輸入、有界輸出穩定性 6.3 有界輸入、有界輸出穩定性與漸進穩定之間的關係 6.4 MATLAB在穩定性分析中的套用 6.5 循序漸進例子:穩定性分析 6.6 習題 第7章 線性狀態反饋控制系統的設計 7.1 狀態反饋控制律 7.2 動態回響設計 7.3 狀態反饋閉環特徵值配置 7.4 可鎮定性 7.5 穩定...
3.4.4系統的零動態和系統的可鎮定性 3.4.5輸出與干擾的解耦控制 3.5小結 第4章多指標非線性控制設計方法 4.1引言 4.2輸出函式在非線性控制設計中的作用 4.2.1輸出函式在SISO系統中的零、極點配置作用 4.2.2輸出函式在MIMO系統中的零、極點配置作用 4.3非線性控制設計中的完全和部分精確線性化問題 4....
(8)一般情況下,正則系統具有滿足Lyapunov意義下的魯棒穩定性和魯棒可鎮定性,而線性奇異系統則不一定滿足。通過上面對線性奇異系統和正則系統的結構特徵的對比分析,我們可以得到結論:線性奇異系統是比正則系統更具有廣泛形式的動力學系統,它較之正則系統具有更加豐富的內涵,其在實際工程中的套用範圍也要廣闊得多,在...
針對非線性奇異攝動系統的穩定性分析問題,相繼提出複合Lyapunov函式法、基於二次型Lyapunov函式的複合Lyapunov函式法以及向量Lyapunov函式法Ⅲ’等。在上述研究的基礎上。進一步研究了系統參數存在不確定性的魯棒穩定性及狀態反饋控制問題、基於S-過程和LMI方法的系統受非線性時變攝動干擾下的二次可鎮定性與非線性PI魯棒...
