基本介紹
- 中文名:可表示擬陣
- 外文名:representable matroid
- 所屬學科:數學
- 別名:可坐標化擬陣
- 所屬問題:離散數學(組合序)
- 簡介:一種組合構形
基本介紹


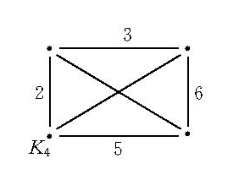
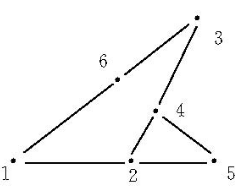
相關介紹













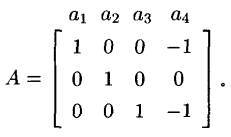









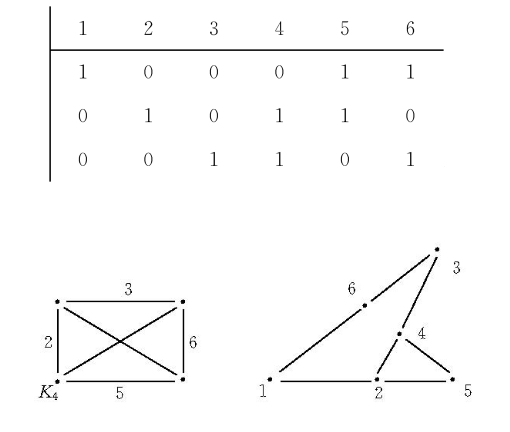


















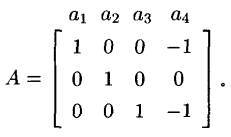









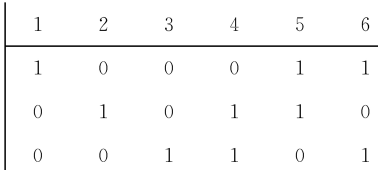
可表示擬陣(representable matroid)亦稱可坐標化擬陣,是一種組合構形,它是與有限域GF(q)上的矩陣擬陣M(A)有一一對應關係的擬陣M(E),稱M(A)為擬陣M(E)的表示,矩陣A為擬陣的表示矩陣。基...
這個擬陣被稱為A的列擬陣,也稱為A表示M。例如,法諾擬陣可以表示為一個3*7的0-1矩陣。列擬陣是向量擬陣的另一種叫法,然而在進行矩陣表示時,這種表達方式更常用。一個等價於向量擬陣的擬陣,儘管其表示可能不同,被稱為可表示的...
單模擬陣亦稱正則擬陣,是一類特殊的可表示的擬陣,指在任何域上均可表示的擬陣。擬陣M(E)為單模擬陣,若且唯若M(E)有全單模的表示矩陣。簡介 單模擬陣亦稱正則擬陣,是一類特殊的可表示的擬陣,指在任何域上均可表示的擬陣。單模...
《基於可表示擬陣的理想的秘密共享方案的研究》是依託華中科技大學,由許靜芳擔任項目負責人的青年科學基金項目。項目摘要 理想的秘密共享方案具有效率最優的特點,它所實現的理想的存取結構的特徵描述是秘密共享領域主要的開放性問題之一,這...
單形擬陣(simplicial matroid)是一類特殊的擬陣,它是以獨立單形為獨立集的擬陣。 中文名 單形擬陣 外文名 simplicial matroid 當單形為k單形時,記單形擬陣為Sk,這裡A一{al,…,a,},以k單形構成的集合{X XZ,...}Xn}的獨立性是由...
對偶擬陣(dual matroid)亦稱正交擬陣,是一種組合構形,它是由擬陣M導出的擬陣M*,當擬陣M以基集族B表示時,M=(E,B),則M*=(E,B*),其中B*={E-B:B∈B}。因此,當B為擬陣M的基時,E-B就是對偶擬陣的基,對於擬陣...
表示由X產生的理想 包含元素的個數,此時 為一多面體擬陣,於是,可由 派生序陣,記為 若且唯若X為P上的一個理想,稱 為偏序集序陣,或時間表序陣。相關介紹 擬陣多面體是一種組合構形,它是由擬陣M=(E,I)的所有獨立集的...
《不含某些子式的擬陣結構》是依託福州大學,由陳容擔任項目負責人的青年科學基金項目。項目摘要 Rota猜想(即對任意的有限域F,F不可表示的最小擬陣個數是有限的。)由Rota在1970年國際數學大會上提出,是擬陣中最基本也是最核心的一...
將A從G中移去以後會增加G的連通分支的數目,正如G的圈構成M(G)的圈一樣,以G的上圈為圈,對應地得到G上的另一類擬陣,稱為上圈擬陣,上圈擬陣亦稱鍵擬陣,圈擬陣和上圈擬陣互為對偶,且在任何域上均可表示,記上圈擬陣為M(G...
在以約束不等式表示的擬陣多面體裡,若以G的滿足下述條件的一般整值次模函式f取代擬陣的秩函式:1.f(∅)=0;2.對於E的任意子集A,B,若A⊆B則:f(A)≤f(B);3.對於E的任意子集A和B,有 則不等式組I(E,f)決定的...
representable,英語單詞,主要用作形容詞,作形容詞時譯為“能被代表的;能上演的;能被描繪的”。短語搭配 representable matroid 可表示擬陣 representable uninorms 表示的統一模 representable functor 可表的函子 representable function ...
例如,E={a,b,c,d,e},獨立集為元素個數不超過3的E的所有子集,若q₁={a,b,c},q₂={a,b,d},q₃={a,b,e},則Q={q₁,q₂,q₃}為此擬陣的截元表示。擬陣的截元表示並不惟一,例如,除Q...
