基本介紹
- 中文名:截元
- 外文名:transverse
- 所屬學科:數學
- 所屬問題:離散數學(組合序)
- 簡介:一種組合構形
基本介紹,相關說明,
基本介紹
截元是與有限集E的給定子集族有特定關係的E的一個子集,對於有限集E={e1,e2,…,en}的特定子集T={ej1,ej2,…,ejt},稱這樣的T為Q的偏截元或相異代表集。若它滿足:
1.T中的元素均不相同;
2.對於由E的子集q1,q2,…,qm構成的集族Q={q1,q2,…,qm},若從指標j1,j2,…,jt出發,可以得到一組互不相同的指標i1,i2,…,it,並使得ejk∈qik,對所有的k (1≤k≤t)均成立,
在這裡允許1≤t≤n,而當t=m時,稱T為Q的截元。例如,若E={1,2,3},q1={1,2},q2={2,3},Q={q1,q2},則T1={1},T2={2},T3={3}均為Q的偏截元,而T4={1,3},T5={2,3},T6={1,2}均為Q的截元。
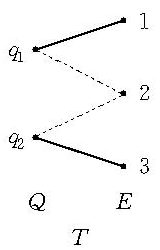
圖1
相關說明
從組合論觀點看,截元相應於二部圖上的匹配,或者說一種對應關係,它把集族歸約為一個更容易處理的集合,容易看到,當T為Q的偏截元時,T的子集仍為Q的偏截元,這種序關係類似於擬陣中獨立集的相應性質,因此,把以偏截元為其獨立集的擬陣,稱為截元擬陣,對於截元擬陣,其對偶擬陣一般不再是截元擬陣,但是,截元擬陣和匹配擬陣本質上是一回事,因為:一個擬陣是匹配擬陣,若且唯若它是截元擬陣,這同時表明截元擬陣在組合論中的重要性。
當在擬陣M=(E,I)和截元擬陣MT之間有一一對應關係時,換言之,對於擬陣M,有|E|=n,此時以E的子集q1,q2,…,qm構成的集族Q={q1,q2,…,qm},使得獨立集族I與Q的偏截元集族一一對應,則稱Q為擬陣M的截元表示。例如,E={a,b,c,d,e},獨立集為元素個數不超過3的E的所有子集,若q1={a,b,c},q2={a,b,d},q3={a,b,e},則Q={q1,q2,q3}為此擬陣的截元表示。擬陣的截元表示並不惟一,例如,除Q以外,E={E,E,E}也是該擬陣的截元表示。一般地,若Q={q1,q2,…,qm}是擬陣的截元表示,則滿足qi⊆Ti⊆E (i=1,2,…,m)的T={T1,T2,…,Tm}也是擬陣的截元表示,藉助於截元表示,可以判定已知擬陣和截元擬陣的關係。若M(E)是秩為k的擬陣,M′(E)為一截元擬陣,且其截元表示為Q={q1,q2,…,qk},則M(E)的每一獨立集亦為M′(E)的獨立集,若且唯若對於{1,2,…,k}的任意子集I,均有


