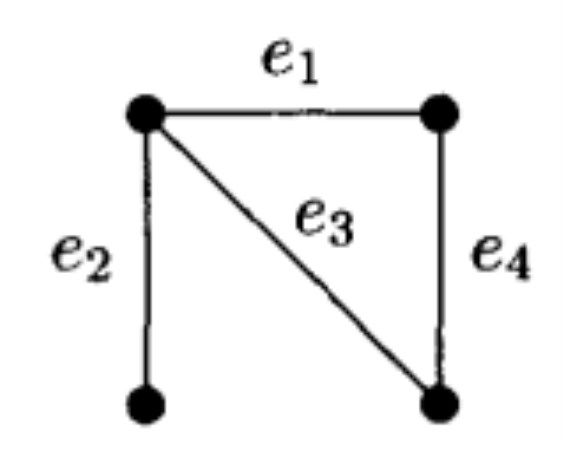
圈擬陣(circuit matroid)亦稱多邊形擬陣,是一類特殊的擬陣,它是建立在圖G=(V,E)上的一類擬陣M(G)。設G是一個圖,E=E(G)是G的邊集。定義I⊆2為這樣的一個集合: X∈I若且唯若X(作為G的子圖)不含有極小圈,那么(E,I)是一個擬陣,這個擬陣通常稱為G的圈擬陣(cycle matroid),記作M(G)。此結論可由以下例子得出:設G是一個圖,其邊集為E=E(G),當X⊆E是G的一個無圈子圖(即不含有極小圈的子圖),則X的任意子集Y也是G的一個無圈子圖。當X1,X2⊆E是G中的兩個無圈子圖並且|X1|<|X2|時,則在G的子圖X1∪X2中, X1也不是X1∪X2的極大無圈子圖。因而有e∈X2-X1,使得X1∪e也是G中的一個無圈子圖。
基本介紹
- 中文名:圈擬陣
- 外文名:circuit matroid
- 所屬學科:數學
- 所屬問題:組合學(組合序)
- 別名:多邊形擬陣
- 簡介:建立在圖G=(V,E)上的一類擬陣
基本介紹
相關性質
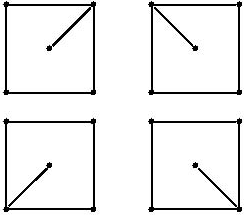
舉例