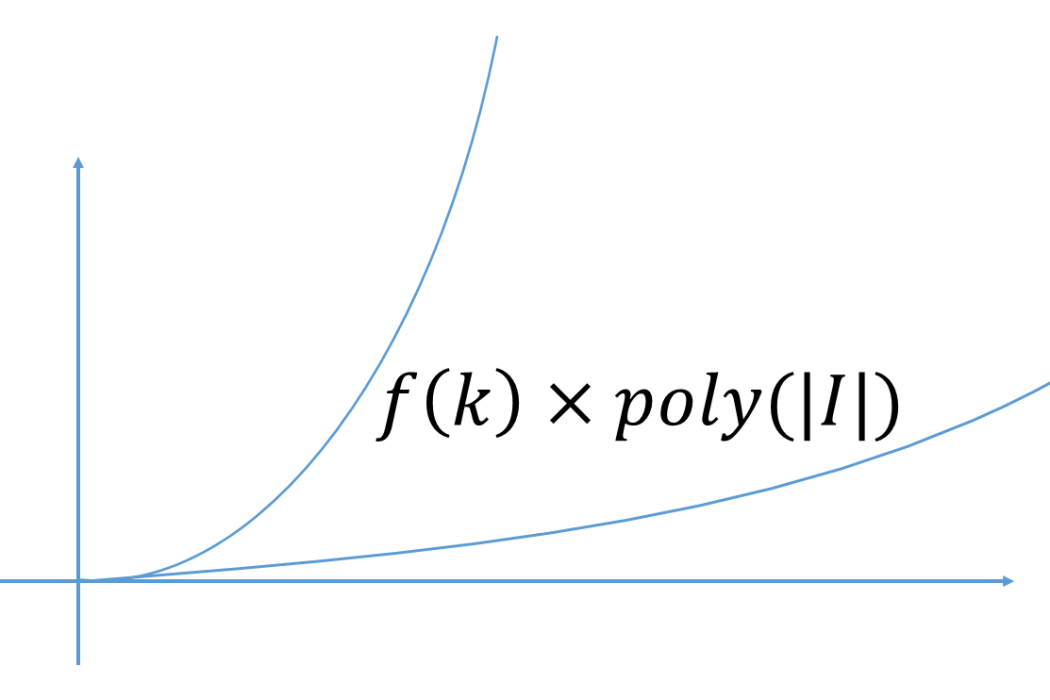參數算法（parameterized algorithm）是基於參數複雜度理論（parameterized complexity）設計的一類算法，其運行時間複雜度可以寫成f(k)*n^c的形式，其中k是我們的參數。參數的選取根據不同的情況而定，通常以解的大小為參數，也可以以樹寬為參數。在參數算法領域，我們一般稱固定參數算法（fixed parameterized algorithm），簡稱FPT。
基本介紹
- 中文名：參數算法
- 外文名：Parameterized Algorithm
- 所屬學科：計算機科學
引言,定義,參數,
引言
許多現實存在的問題都是NP完全問題，例如：TSP問題，點覆蓋問題，整數規劃等。從目前的情況看，這些問題是不太可能找到一個多項式運行時間的算法（
）。若用n代表其輸入大小，以上這些問題的精確算法的時間複雜度可以表示為
，其中c是一個大於1的常數。這種指數類型的算法在實際中很難得到運用，因為運行時間會隨著問題規模的增長產生指數爆炸。因此，對於NP完全問題，學者從參數複雜度的角度進行算法設計分析。
參數算法的初衷是，通過在問題中引入一個參數k，將算法的時間複雜度的指數部分限制在參數k上而不是整個輸入大小n，只要參數k的大小控制在一定範圍之內，算法的時間複雜度依然是整個問題輸入的多項式。通過這種方法可以把一大批NP完全問題的可解範圍擴大很多。
定義
下面給出參數算法的正式定義：
如果某個算法的時間複雜度具有如下形式：
，則稱該算法為固定參數算法（fixed-parameter algorithm），或者FPT算法。其中k是問題的參數，n是問題的輸入的大小，c是一個獨立於k和n的常數，f(k)是以k為自變數的可計算函式。
參數算法的設計目標有兩個，降低算法運行時間的指數部分和降低算法運行時間的多項式部分。目前大多數研究者的研究興趣主要集中在降低算法運行時間的指數部分。
參數
選擇恰當的參數是參數算法的設計過程中的一個重要問題。
一種常見的參數選擇方式是以解集的大小k為參數。如對於點覆蓋（Vertex Cover）問題，加入解集的大小k作為參數後問題描述變為：輸入的圖G中是否存在解集大小不超過k的點覆蓋。這個問題可以在
時間內被解決。
當然，參數的選擇是多種多樣的，恰當參數的選擇可以體現出算法設計者的水平與功底。除了以解集的大小k為參數外，還有許多其他的參數選擇方法，如在圖算法中以某種結構參數作為參數，例如以treewidth作為參數。
