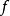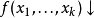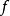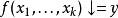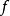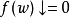在可計算性理論中，可計算函式（computable function）或圖靈可計算函式是研究的基本對象。它們使我們直覺上的算法概念更加精確。使用可計算函式來討論可計算性而不提及任何具體的計算模型，如圖靈機或暫存器機。但是它們的定義必須提及某種特殊的計算模型。
在可計算函式的精確定義之前，數學家經常使用非正式術語可有效計算的。這個術語因此可以被認同為可計算函式。儘管這些函式被叫做有效的，它們可能極其困難。可行可計算性和計算複雜性研究可有效計算的函式。
依據邱奇-圖靈論題，可計算函式精確的是使用給出無限數量的時間和存儲空間的機器計算設備來計算的函式。等價的說，這個論題聲稱有算法的任何函式都是可計算的。
可以使用 Blum 公理來在可計算函式的集合上定義抽象計算複雜性理論。在計算複雜性理論中，確定一個可計算函式的複雜性的問題叫做功能性問題。
基本介紹
- 中文名：可計算函式
- 外文名：computable function
- 套用學科：數學
- 相關術語：邱奇-圖靈論題
- 又名：圖靈可計算函式
- 所屬領域：數學
定義,可計算集合,形式語言,例子,
定義
計算函式是在自然數上的有限偏函式。每個可計算函式
接受固定數目個自然數作為參數；不同的函式接受不同數目的參數。因為函式是部分的，它們可以不定義在所有可能的輸入選擇上。如果定義了一個可計算函式，則它返回一個單一自然數作為輸出（這個輸出可以被解釋為使用配對函式的一列數）。記號
指示偏函式被定義在參數
上，而記號
指示被定義在參數上而返回的值是y。這些函式也叫做偏遞歸函式。在可計算理論中，函式的定義域是函式被定義在其上的所有輸入的集合。
定義在所有參數上的函式叫做全函式。如果可計算函式是全函式，它叫做全可計算函式或全遞歸函式。
有很多等價方式定義可計算函式的類。為了具體，本文餘下部分將假定可計算函式已經被定義可以被圖靈機計算的那些偏函式。有很多計算的等價模型定義同一類可計算函式。這些計算模型包括
- Mu-遞歸函式
- Lambda演算
- Post機，也叫做標記系統
等等。
可計算集合
自然數的集合A被叫做可計算的（同義詞：遞歸的，可決定的），如果有可計算函式f使得對於每個自然數n，
如果n在A中，並且
如果n不在A中。
自然數的集合被叫做計算可枚舉的（同義詞：遞歸可枚舉的，半可判定的），如果有可計算函式f使得對於每個自然數n，f(n)是有定義的，若且唯若n在這個集合中。所以一個集合是計算可枚舉的，若且唯若它是某個可計算函式的定義域。使用詞可枚舉的因為對於自然數的非空子集B下列是等價的：
- B是可計算函式的定義域。
- B是全可計算函式的值域。如果B是無限的則這個函式可以被假定為單射的。
如果集合B是函式f的值域，則這個函式可以被看作B的枚舉，因為列表f(0),f(1), ...將包含B的所有元素。
因為在自然數上的每個有限關係都可以被識別為對應的自然數的有限序列的集合，可計算關係和計算可枚舉關係的概念可以從它們的集合類似物來定義。
形式語言
在計算機科學的可計算性理論中，經常考慮形式語言。它包括任意集合的一個字母表，在字母表上的字是來自字母表的符號的有限序列；同一個符號可以出現多於一次。例如，二進制字元串精確的是在字母表
上的字。語言是在固定字母表上的所有字的蒐集的子集。例如，精確的包含三個字母的所有二進制字元串的蒐集是在二進制字母表上的一個語言。
形式語言的一個關鍵性質是對判定一個給定字是否在這個語言中的難度級別。必須開發某種編碼系統來允許可計算函式來接受在語言中的任意字作為輸入；這通常是要認真處置的例程。一個語言被稱為是可計算的（同義詞：遞歸的，可判定的），如果存在一個可計算函式
使得對於在字母表上的每個字w，
如果這個字在這個語言中，並且
如果這個字不在這個語言中。所以一個語言在有一個過程能正確的判定任意的字是否在這個語言中的情況下是可計算的。
一個語言是計算可枚舉的（同義詞：遞歸可枚舉的，半可判定的），如果有可計算函式f使得
是有定義的，若且唯若字w在這個語言中。術語可枚舉同自然數的計算可枚舉集合有同樣的語源。
例子
如果f和g是可計算的，則：f + g,f * g, 
如果f是一元的，max(f,g), min(f,g)和更多的組合都是可計算的。
