1796年3月30日是一個關鍵時候,當年高斯才18歲,他發現了如何從“歐氏工具”,也就是以圓規及直尺,作十七邊形的圖。這個發現使高斯在數學家中一炮而紅,也因這事件使高斯決定獻身數學。
高斯對此成就是那么自豪與高興,因而告訴他的友人說,他的墓碑上一定要刻上正17邊形,可惜並沒有如願以償,高斯的紀念碑上刻著一個十七個角的星星,原來是負責紀念碑的雕刻家認為正十七邊形和圓形太像了,大家一定分辨不出來。
基本介紹
- 中文名:十七角星
- 外文名:17 points star
- 提出者:卡爾·弗里德里希·高斯
- 提出時間:1796年3月30日
- 套用學科:數學
發明者簡介,正十七角星作法,步驟一,步驟二,步驟三,簡易作法,相關小故事,相關理論,
發明者簡介
卡爾·弗里德里希·高斯,德國著名數學家、物理學家、天文學家、大地測量學家。和牛頓、阿基米德,被譽為有史以來的三大數學家,是近代數學奠基者之一,18歲時發現了質數分布定理和最小二乘法。通過對足夠多的測量數據的處理後,可以得到一個新的、機率性質的測量結果。在這些基礎之上,高斯隨後專注於曲面與曲線的計算,並成功得到高斯鐘形曲線(常態分配曲線)。其函式被命名為標準常態分配(或高斯分布),並在機率計算中大量使用。1799年高斯於黑爾姆施泰特大學因證明代數基本定理獲博士學位。從1807年起擔任哥廷根大學教授兼哥廷根天文台台長直至逝世。高斯的肖像已經被印在從1989年至2001年流通的10元面值德國馬克的紙幣上。
正十七角星作法
先計算或作出cos(360°/17)
設正17邊形中心角為a,則17a=360°,即16a=360°-a
故sin16a=-sina,而
sin16a=2sin8acos8a=4sin4acos4acos8a=16sinacosacos2acos4acos8a
因sina不等於0,兩邊除之有:
16cosacos2acos4acos8a=-1
注意到cos15a=cos2a,cos12a=cos5a(誘導公式)等,有
2(cosa+cos2a+…+cos8a)=-1
令
x=cosa+cos2a+cos4a+cos8a
y=cos3a+cos5a+cos6a+cos7a
有:
x+y=-1/2
又xy=(cosa+cos2a+cos4a+cos8a)(cos3a+cos5a+cos6a+cos7a)
=1/2(cos2a+cos4a+cos4a+cos6a+…+cosa+cos15a)
經計算知xy=-1
因而:x=(-1+√17)/4,y=(-1-√17)/4
其次再設:x1=cosa+cos4a,x2=cos2a+cos8a
y1=cos3a+cos5a,y2=cos6a+cos7a
故有x1+x2=(-1+√17)/4
y1+y2=(-1-√17)/4
最後,由cosa+cos4a=x1,cosacos4a=(y1)/2
可求cosa之表達式,它是數的加減乘除平方根的組合, 故正17邊形可用尺規作出
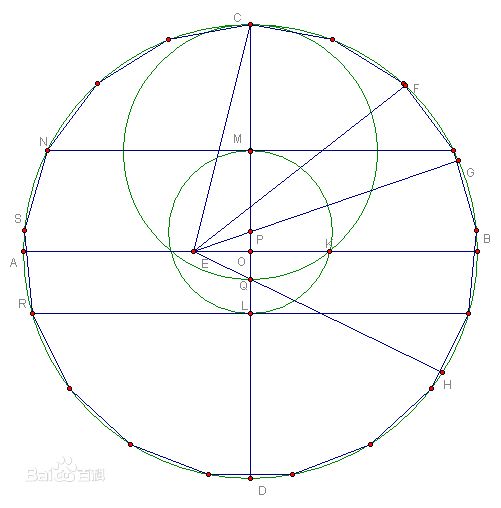
步驟一
給一圓O,作兩垂直的半徑OA、OB,
在OB上作C點使OC=1/4OB,
在OA上作D點使∠OCD=1/4∠OCA 作AO延長線上E點使得∠DCE=45度。
步驟二
作AE中點M,並以M為圓心作一圓過A點,
此圓交OB於F點,再以D為圓心,作一圓
過F點,此圓交直線OA於G4和G6兩點。
步驟三
過G4作OA垂直線交圓O於P4,
過G6作OA垂直線交圓O於P6,
則以圓O為基準圓,A為正十七邊形之第一頂點P4為第四頂點,P6為第六頂點。
以1/2弧P4P6為半徑,即可在此圓上截出正十七角星的所有頂點。
簡易作法
因為360°/17≈21°10′ ,利用sinA 21°6′=0.3600可得近似角。用該方法作正十七邊形總誤差為17*4′=68′,在不要求十分精確的情況下還是可行的。 作法如下:1.先畫一條直線,用圓規在上面截取5條相等線段,(儘量越短越好),再截取之前四條線段的和,接續之前畫的線段。這樣,如果每條小線段算作0.1的話,那么整條線段就是1.8。 2.用圓規截取之前5條小線段的長,畫5次,這樣這條線段就是5。1.8/5=0.36。準備工作完畢! 3.另作一條直線,作垂線,1.8的線段作為對邊,5的線段作為斜邊,那個最小的銳角即是近似的360°/17的角。以其頂點為圓心,重複作角直至閉合。畫一大圓,連線其與17條射線的交點,即可。
相關小故事
大多數的同學認識數學王子—高斯(GAUSS.德國數學家西元1777年~1855年)是由國中數學課本講等差級數時有這一則故事。據說高斯在幼年時,老師出了一道複雜的計算題,即「求由1到100所有整數和」,但高斯卻令人驚訝的在幾秒內就算出它的正確答案為〝5050〞。這使他的老師再也不敢看不起鄉下小孩,進而使老師更賣力地幫助高斯,直到他無法教給高斯更進一步的數學知識。
相關理論
高斯不但解決了正十七邊形的作圖問題,而且也知道在理論上,用圓規和直尺作圖,哪些正多邊形可以做到,哪些是不能做到。他的定理說: