加伯轉換

加伯變換是窗函式為高斯函式的短時距傅立葉變換。

基本介紹

• 中文名：加伯轉換
• 領域：數學

數學定義

將短時距傅立葉變換中的窗函式代入高斯函式，即可得下面的定義。

根據高斯函式會從兩側遞減的性質，我們可以將上式進一步化簡：

讓積分範圍不是無限大，有利於實作。

為何選擇高斯函式作為窗函式

1. 其他窗函式的短時距傅立葉變換，如短時距傅立葉變換提到的方形窗函式，無法同時兼顧時間軸和頻率軸的解析度；一者解析度提升，另一者解析度必定下降。但高斯函式由海森堡測不準原理可得知，是最能同時讓兩軸兼顧解析度的窗函式(將於下個章節詳述)。
   
2. 高斯函式為傅立葉轉換的特徵函式，因此經過轉換後其性質不變。因此可讓加伯變換後在時間軸和頻率軸的性質相互對稱。
   

加伯變換的一般化

由於高斯窗函式的寬度可以由其變異數做調整，因此我們將這個參數加入加伯變換的數學式子中，讓轉換更加彈性。

改變高斯函式的寬度，和改變方形窗函式短時距傅立葉變換的效果類似。若選取較大的 ，高斯窗函式較窄，則時間軸有較高的解析度，頻率軸的解析度會下降。反之，若選取較小的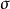 ，高斯窗函式較寬，則時間的解析度下降，頻率軸的解析度會上升。雖然還是有兩軸之間的解析度的犧牲，但比起其他無法滿足測不準原理下限的窗函式，加伯變換的兩軸還是能相對維持較高的解析度。

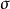
離散Gabor變換

Gabor表示的離散版本

通過在這些方程中離散Gabor基函式，可以很容易地推導出。由此，連續參數t被離散時間k代替。此外，必須考慮Gabor表示中現在的有限求和極限。以這種方式，採樣信號y（k）被分成長度為N的M個時間幀。根據，臨界採樣的因子Ω是

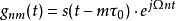
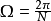
類似於DFT（離散傅立葉變換），獲得分成N個離散分區的頻域。然後，這N個頻譜分區的逆變換導致時間窗的N值y（k），其由N個樣本值組成。對於具有N個樣本值的整個M時間視窗，每個信號y（k）包含K = N·M個樣本值:(離散Gabor表示）

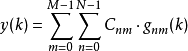
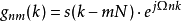
根據上面的等式，N·M係數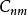對應於信號的樣本值K的數量。

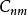
對於過採樣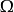設定為與N '> N，其導致離散Gabor表示的第二和中的N'> N個求和係數。在這種情況下，獲得的Gabor係數的數量將是M·N'> K.因此，可獲得比樣本值更多的係數，因此將實現冗餘表示。

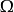
套用例子

Gabor變換的主要套用用於時頻分析。以下面的等式為例。當t≤0時，輸入信號具有1Hz頻率分量，當t> 0時，輸入信號具有2Hz頻率分量

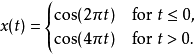
但如果可用的總頻寬是5Hz，則除了x(t)之外的其他頻帶被浪費。通過套用Gabor變換進行時頻分析，可以知道可用頻寬，並且可以將這些頻帶用於其他套用並節省頻寬。右側圖片顯示輸入信號x(t)和Gabor變換的輸出。正如我們所期望的那樣，頻率分布可以分為兩部分。一個是t≤0而另一個是t> 0.白色部分是x(t)占用的頻帶，不使用黑色部分。注意，對於每個時間點，存在負（上白部分）和正（下白部分）頻率分量。