基本介紹
- 中文名:分段可微函式
- 外文名:piecewise differentiable function
- 所屬學科:數學(微分學)
- 屬性:可微函式的推廣
- 相關概念:連續函式,導數,可導,可積等
基本介紹,導數,可微與分段可微,相關結論,
基本介紹
導數
現在複習一下導數的概念:如果差商極限














可微與分段可微
如果函式 在閉區間
在閉區間 的每點有導數(在
的每點有導數(在 點只要右導數,在b點只要左導數),就說
點只要右導數,在b點只要左導數),就說 在區間
在區間 可微。其直觀意義就是
可微。其直觀意義就是 的圖象在
的圖象在 上處處有確定的切線。
上處處有確定的切線。







可以把在區間的可微推廣為分段可微:如果能把閉區間 分成有限多個閉區間,使
分成有限多個閉區間,使 分別在每個小的閉區間上可微,就說函式
分別在每個小的閉區間上可微,就說函式 在
在 上分段可微。例如圖1就表示一個在
上分段可微。例如圖1就表示一個在 上分段可微的函式,分開的小閉區間就是
上分段可微的函式,分開的小閉區間就是 ,這樣分開的小的閉區間叫做
,這樣分開的小的閉區間叫做 的可微區間。
的可微區間。







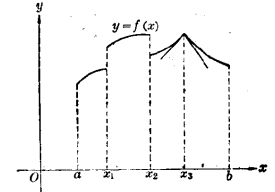 圖1
圖1如果 在整個數軸上有意義,且在數軸上的任何閉區間(長度有限)上分段可微,就說
在整個數軸上有意義,且在數軸上的任何閉區間(長度有限)上分段可微,就說 在整個數軸上分段可微。
在整個數軸上分段可微。


分段可微函式不但可能有有限跳躍,而且其圖象可能有“尖點”,即左、右導數存在但不相等的連續點(如圖1中 處)。
處)。

相關結論
關於分段連續
(1)如果 在數軸上分段連續,它在任何閉區間
在數軸上分段連續,它在任何閉區間 上分段連續,就是說,可把
上分段連續,就是說,可把 分成有限多個小的閉區間,
分成有限多個小的閉區間, 分別在這些小的閉區間上連續。這樣,
分別在這些小的閉區間上連續。這樣, 就分別在這些連續區間上可積,從而
就分別在這些連續區間上可積,從而 在
在 可積。
可積。







(2)如果 在數軸上分段連續,那么,在它的連續區間內部的點上,
在數軸上分段連續,那么,在它的連續區間內部的點上, 的極限存在,即左、右極限都存在且相等。在連續區間的右端點,例如在圖1中區間
的極限存在,即左、右極限都存在且相等。在連續區間的右端點,例如在圖1中區間 的右端點
的右端點 ,
, 的左極限
的左極限 存在。但
存在。但 同時是右方相鄰的連續區間
同時是右方相鄰的連續區間 的左端點,故在
的左端點,故在 的右極限
的右極限 也存在。總而言之,在數軸上的任何點
也存在。總而言之,在數軸上的任何點 ,分段連續函式
,分段連續函式 的左、右極限
的左、右極限 都存在。
都存在。 在
在 唯一可能的間斷性是
唯一可能的間斷性是 ,這種間斷性稱為有限跳躍。分段連續函式不能具有象
,這種間斷性稱為有限跳躍。分段連續函式不能具有象 在
在 那樣的間斷性。
那樣的間斷性。


















分段可微函式
(3)如果 在數軸上分段可微,則它在可微區間上必連續,於是
在數軸上分段可微,則它在可微區間上必連續,於是 在數軸上分段連續,根據(1),知
在數軸上分段連續,根據(1),知 在任何閉區間上可積。
在任何閉區間上可積。



(4)通過類似(2)中的討論可知,如 在數軸上分段可微,則在數軸上的任何點
在數軸上分段可微,則在數軸上的任何點 都具有左導數
都具有左導數 和右導數
和右導數 。
。




(5)設 只是在長為T的區間
只是在長為T的區間 上給出的分段可微函式,把
上給出的分段可微函式,把 按周期T延拓到整個數軸上(仍用
按周期T延拓到整個數軸上(仍用 表示延拓後的函式)。那么,延拓後的
表示延拓後的函式)。那么,延拓後的 必是數軸上分段可微的函式。這時
必是數軸上分段可微的函式。這時 。
。







