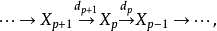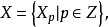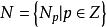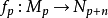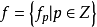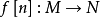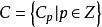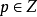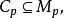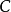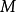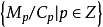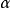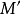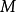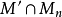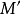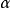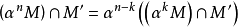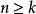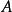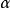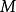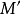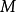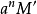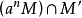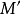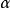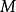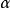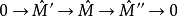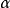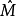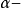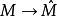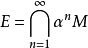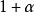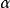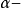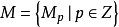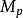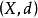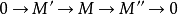分次模

分次模(graded module)是具有分次結構的分次環上的模，是同調代數的基本概念之一，指由一些A模所組成的序列。類似於分次環，在分次模中可定義g分支、g次齊次元和g次齊次分量。分次模M的支集規定為{M_g≠0|g∈G}，並記為Supp_G(M)。M的G分次子模N，是指N為M的R子模且N=⊕_g∈G(N∩M_g)，這等價於若x∈N，則x的齊次分量也在N中，特別地，R^R的分次子模稱為R的分次左理想，類似地，可定義R的分次右理想和分次理想。

基本介紹

• 中文名：分次模
• 外文名：graded module (in homological algebra
• 屬性：同調代數的基本概念之一
• 所屬學科：數學
• 相關概念：分次環、分次子模等

基本介紹

分次模(graded module (in homological algebra) )是同調代數的基本概念之一，指由一些A模所組成的序列。稱為一個(單)分次模，其中均為A模，環A上的一個復形

若不考慮邊緣同態d，則決定一個分次模若也是一個分次模，n是一個固定的整數，則模同態的集合稱為由M到N的n次的分次模映射，這個映射常表成。若分次模中，對每個都有稱為的分次子模，而分次模稱之為它們的分次商模。模範疇中所有的分次模連同分次模映射構成一個阿貝爾範疇。

相關

①A是Noether 環，M是有限生成的A-模，是M的一個-濾鏈，則下述論斷等價：

i)是有限生成-模；

ii) 濾鏈是穩定的。

②(Artin-Rees引理)設A是Noether環，是A的一個理想，M是一個有限生成的A-模，是M的一個穩定-濾鏈，設是的一個子模，則是的一個穩定-濾鏈。

③存在整數k，使得，對一切。

④設是Noether環，是一個理想，是一個有限生成A-模，是的一個子模，則濾鏈和具有有界差。特別，的-拓撲與由的-拓撲所誘導出的拓撲相同。

⑤設

是Noether 環A上有限生成的正合序列是，是A的理想，則-adic完備化序列

是正合的。

⑥設A是Noether環，是一個理想M是有限生成A-模，是M的完備化，則的核由M中被中某元素所零化的那些元素x組成。

⑦A是Noether環，是A的一個包含在大根中的理想。M是有限生成A-模，則M的拓撲是Hausdorff 拓撲，即。

⑧設A是Noether局部環，m是它的極大理想，M是有限生成A-模，則M的m-拓撲是Hausdorff 拓撲，特別A 的m-拓撲是Hausdorff 拓撲。