分析組合學

分析組合學以生成函式為核心，套用分析學的方法對有各種結構的組合對象的性質進行精確的預測，是組合數學中重要的分支。

分析組合學首先是由對象的組合結構的描述，對象的內在結構決定了其生成函式，這時的生成函式只是形式上的；接著，生成函式被視為分析學的對象，其變元在複數域上變化，而生成函式則定義了一個複平面到自身的映射，複分析中的理論得以漸進地得到對象的性質，比如奇點往往漸進地決定了級數係數，從而得到計數的精確估計。這樣的推理適用於組合數學中一大類對象，比如字、組成、拆分、樹、排列、圖、映射等等。該方法稍作改動，即可適用於隨機結構的量化分析，比如通過擾動的方式。

分析組合學的最早的開拓者有萊昂哈德·歐拉、凱萊、拉馬努金、波利亞，20世紀隨著計算機技術發展，算法及大量複雜數據結構研究的深入，分析組合學被更廣泛地研究和套用，其要義可以在Knuth的《電腦程式設計藝術》中看到，Flajolet，Sedgewick則在《分析組合學》中深入探討了分析組合學的幾個內容。

基本介紹

• 中文名：分析組合學
• 外文名：Analytical Combinatorics

基本內容

分析組合學主要是分為兩個階段，分別是符號化方法和利用複分析方法對符號化方法得到的結果進行漸進分析。分析組合學的核心是生成函式，在符號化方法中其變元是形式上的，而在漸進分析時，則是複數域上的。

符號化方法利用了組合學對象的內在結構，派生出相應的生成函式。組合對象主要分兩類，一是無標號對象，即組成對象的元素之間不加區分；二是有標號對象，即組成對象的元素之間是嚴格區分開的。前者的對應普通的生成函式，而後者則對應於指數型生成函式。對象的結構往往具有普遍性，具有代表性的就是不相交並、笛卡爾積、序列、多重集、冪集、環等等，更為複雜的結構則基於對稱群的波利亞理論。符號化方法常常代替遞歸式，直接由對象的組成結構派生出相應的生成函式，從而輕而易舉地解決經典組合學中棘手的問題。

漸進分析是分析組合學的另一方面內容。符號化方法得到的生成函式是形式冪級數，它並不在乎級數是否收斂，然而一旦要研究這個級數的係數序列的性質，就必須把其中的變數放到複數域上來看。儘管在部分情況下可以由生成函式直接得到其係數的準確表達，但是更多數情況下，係數並不能直接解析地得到，比如生成函式是在一個函式方程中隱式定義了，或者這個生成函式如此複雜，以至於我們只能期求得到它的一個良好的估計。奇點法、鞍點法就是解決此類問題的重要手段。

以下我們重點介紹“組合結構”，簡單介紹漸進分析。

符號化方法

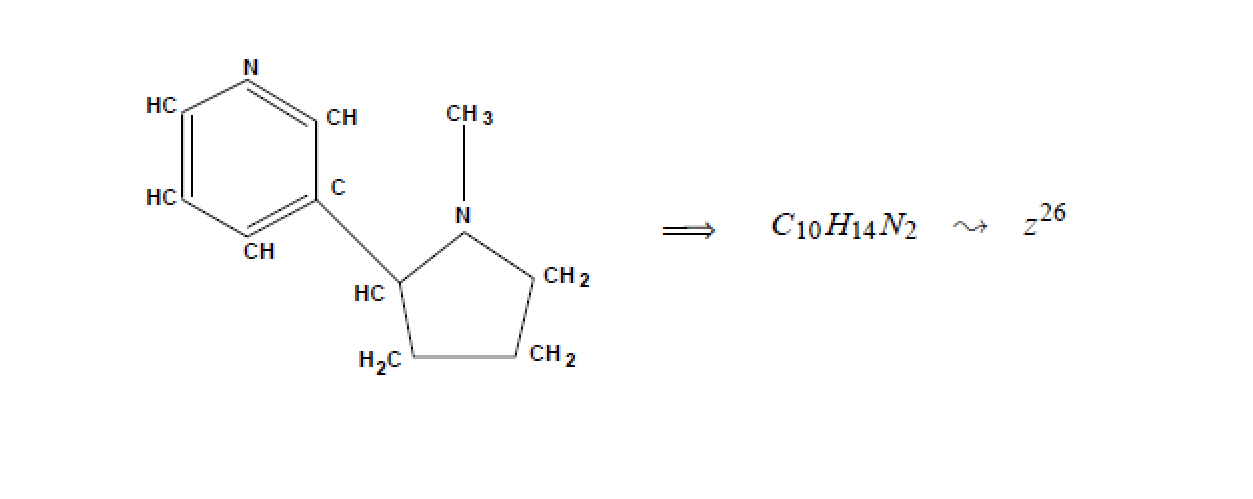
不同的組合結構往往對應不同的生成函式。何為組合結構？我們知道任何待計數的對象可以分解成更小的原子，原子按照某種結構組合得到待計數的對象。受化合物的表示啟發，比如對於一個分子，我們這樣表示：

有複雜結構的分子化合物就被一個簡單的變數z表示了，這時單個的組分（CH、CH₂、CH₃）都被視為了原子z。

分析組合學

對於複雜結構的計數可以藉助波利亞理論，我們這裡只舉幾個簡單的結構結論，其中無標號對象和帶標號對象對應了兩種不同的生成函式：普通型生成函式和指數型生成函式。由對象內在結構得出生成函式的過程稱為符號化方法。

結構1：無標號對象

定義1.1：一個組合類，或簡單的類，是在一個有限或可數的集合上定義了一個大小size函式，它滿足以下的條件：

（i）元素的大小是非負整數；

（ii）任一給定大小的元素數目是有限的。

如果A是一個類，任一α∈A由|α|_A表示，或簡寫成|α|，用A_n表示A中的大小等於n的元素集合，用a_n表示card(A_n)，我們說|·|定義了一個從A上元素到Z_≥0的映射，a_n則表示了A上的計數序列。兩個組合類A和B在組合學意義上是同構的，如果它們的計數序列是一樣的，或者說存在一個從A到B的雙射，保持了大小。

這樣普通生成函式就被定義為：

定義1.2：一個序列a_n的生成函式就是形式冪級數：

或者，等價的，由前面的定義可以有：

也就是通過生成函式變數z標記了A中元素的大小。

針對這樣的冪級數，我們也寫有：

如果原子之間的組合是可接受的構造（以下所談論的都是可接受的），那么可以將對象的組成結構直接翻譯成生成函式。

1. 笛卡爾積：兩個類B和C的笛卡爾積組成一個有序對：

其中

翻譯到生成函式，我們立刻有：

2. 不相交並：如果對組合類A，B，C滿足

|·|定義為對任一 ，

則同樣立刻有：

進一步，使用類的不相交並和笛卡爾積，結合波利亞理論，我們可以得到下面結論，這些結論在Analytical combinatorics中作為一種基本的構造，在此一併引述：

3. 序列：如果B是一個類，那么B構成的序列SEQ(B)被定義為無窮和式：

對應的生成函式為：

比如，非負整數 可以認為是 ，而k的個數就是 前的係數，也就是1；再比如，用{0,1}組成的長度為n的字元串個數，字元串全體同構於

4. 冪集：A=PSET(B)是B的冪集，被定義為B的所有子集構成的集合，圍繞每個元素取和不取，有

簡單譯為：

5. 多重集：對有限集B（這裡必須有 ），將B上的多重集（即元素不必互異）A=MSET(B)是良定義的：

所以

比如考慮正整數的拆分，即正整數n能以幾種方式拆分成若干正整數之和（不考慮整數間順序），這時問題即

6. 環：環要考慮到旋轉的不變性，對A=CYC(B)，有結論：

這裡 是數論中的歐拉函式。可以用波利亞理論證明它。

與序列、冪集、多重集、環相關的運算元，又稱為是波利亞運算元。

無標號對象的可接受構造，很大程度和一類稱為正則語言或是有窮自動機的表示相關，這往往對應於直接由語言翻譯成為生成函式。更為一般的，則涉及一類稱為與上下文無關文法對應的語言，這部分構造的可接受性和形式語言中的Chomsky理論密切相關，比如二叉樹就是上下文無關的，如果定義二叉樹的集合為B，Z表示單個節點，那么二叉樹的語言就是： ，和遞歸定義相關。我們考慮廣義平面樹所成的類G，可以認為是多叉樹，並且子樹的不同排列對應不同的樹，這時，可以輕易寫出：

從而立即有生成函式：

解得

所以大小為n的廣義樹的數目為：

這是無標號對象，對象之間沒有區分，下面考慮帶標號的對象。

結構2：帶標號對象

很多組合學對象自然地具備帶標號的組合結構，即組成對象的每一個原子之間被它們的獨特的標號所區分，這經常和排列相關。比如說，一個排列可以認為是一些互不相同的整數的線性排布。

帶標號的結構上的操作基於一種特殊的乘積：帶標號的乘積，用於將標號在元素間重新分配。對應到指數型生成函式上，就是二項式卷積。帶標號的構造對應於指數型生成函式，無標號對象中的概念稍作改動就可以完全套用到有標號對象的結論上。

定義2.1 一個弱標號的大小為n的對象，指的是其每個節點都是互不相同的整數；而所謂的良標號，則是指大小為n的對象，其標號取自區間[1..n]，且是弱標號的。帶標號的類由良標號的對象組成。

定義2.2 序列( )的指數型生成函式是形式冪級數：

也等價於寫成：

z標記了大小。並且有：

定義2.3 標號類B和C的乘積，記為 ，是分兩步來完成的，先是構作有序對 ，然後在有序對上執行重標號，重標號必須保證B、C內部的標號序仍然和之前一致。

相應的， 的序列滿足二項卷積：

所以

我們繼續如無標號對象般得出幾種常用的構造：

1. 和：

2. 乘積：

3. 序列：

4. 集合：

5. 環：

漸進分析

這裡主要考慮發散級數的漸進分析。在這方面里，很有代表性的就是斯特林公式，

Graham、Knuth、Patashinik的Concrete Mathematics中詳細介紹了利用歐拉——麥克勞林積分公式，拉普拉斯方法估計等等漸進分析方法，拉馬努金有關級數估計中的一類被Knuth稱作是Q函式，其漸進、分布性質也常被用於分析。而事實上，當z作為復變數時，更高深的複分析可以被利用來給出序列漸進性的良好估計，Flajolet、Sedgewick的著述中介紹了基於奇點和鞍點的一系列方法。這裡僅僅就奇點的問題給一些感性的認識。

例1. 假定有這樣一種排列，限制它滿足這樣一種性質：第一個元素小於第二個，第二個大於第三個，第三個則小於第四個，依次類推。這個排列中的數交替的增減，比如(4,8,6,7,5,9,1,3,2)就是滿足該性質的1~9的一個排列，我們稱之為“交錯排列”。觀察n取奇數的情況，n=1,3,5，...,15，得到的序列分別是：

1,2,16,272,7936,353792,22368256,1903757312

如果將它視為有標號的二叉樹的話，可以使用符號化方法得到其指數型生成函式為 。我們需要藉助漸進分析得到序列的性質。從奇點的觀念考慮，看到 正是主奇點，這使得我們有理由認為，可以把 在 附近近似成：

抽取其係數就得到：

（n為奇數）

例2. 我們知道二叉樹的計數，結論是經典的卡特蘭數，

一旦利用斯特林公式，我們就能得到：

我們可以從生成函式的奇點中找到導致此結論的原因。因為生成函式：

我們得到：

複平面上，根式中是多葉的，所以 是奇點，這個奇點的奇性和多項式極點的奇性不同，在適當的條件下，一個平方根奇點 總會牽涉到漸進的形式： 。這也就解釋了卡特蘭數的漸進形式。

一旦利用符號化方法得到生成函式，分析學的方法就可以立刻使用，得到係數的漸進性質，因為大部分組合計數問題的解析解難於表示或者難於估計，此時分析組合學的方式就能夠快速得到解的良好估計。