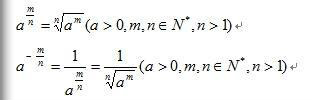分數指數冪

分數指數冪是正分數指數冪和負分數指數冪的統稱。

分數指數冪是一個數的指數為分數，正數的分數指數冪是根式的另一種表示形式。負數的分數指數冪並不能用根式來計算，而要用到其它算法，是高中代數的重點。

基本介紹

• 中文名：分數指數冪
• 領域：數學
• 是：一個數的指數為分數
• 另一種表示法：正數的分數指數冪
• 學科：代數

簡單介紹

分數指數冪是一個數的指數為分數，如2的1/2次冪就是根號2。

分數指數冪是根式的另一種表示形式，

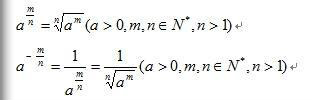
即n次根號(a的m次冪)可以寫成a的m/n次冪。

冪是指數值，如8的1/3次冪=2

一個數的b分之a次方等於b次根號下這個數的a次方

重點：

1、分數指數冪的含義的理解。

2、根式與分數指數冪的互化。

3、有理指數冪的運算性質。

難點：

1、分數指數冪概念的理解。

2、有理指數冪的運算和化簡

證明

a^m/n = ( a^m) 開n 次方 ， （a>0,m、n ∈Z且n>1）

證：
令 ( a^m) 開n 次方 = b
兩邊取 n次方，有
a^m = bⁿ
a^m/n= a^m(1/n) = ( bⁿ)^(1/n) = b = a^m開n 次方
即 a^m/n = ( a^m) 開n 次方

意義

規定：正數的正分數指數冪的意義是——a的n分之m次方=n√a的m次方（a>0,m、n屬於正整數，n>1）

0的正分數指數冪等於0，0的負分數指數冪沒有意義

指出：規定了分數指數冪的意義後，指數的概念就從整數指數推廣到了有理數指數，那么整數指數冪的運算性質也同樣可以推廣到有理數指數冪．

運算性質：

對於任意有理數r,s,均有下面的運算性質

(1)a^r×a^s=a^(r+s) (a>0,r,s∈Q)

(2) (a^r)^s=a^rs (a>0,r,s∈Q)

(3) (ab)^r=a^r×b^r (a>0,b>0,r∈Q)

根式與分數指數冪的互化：

這部分經常弄錯。根號左上角的數當分數指數冪的分母，根號裡面各個因式或因數的指數當分數指數冪的分子，注意，各個因式（因數）如果指數不同，要分開寫。即是內做子，外做母，同母可不同子。

有理指數冪的運算和化簡：

第一步是找同底數冪，調換位置時注意做到不重不漏，接著就是合併同類項，同底數冪的相乘，底數不變，指數相加，相除的話就是底數不變，指數相減。同底數冪相加減，能化簡的合併化簡，不能的按照降冪或升冪排列。

用電腦利用分數指數冪進行多次根號計算：

在查看中，改為“科學型”。先輸入底數，再按“y^x”，接下來如果是3次根號邊輸入“3”“1/x”，以此類推。最後按等於得出結果。實例：27的三次根號，“27”“y^x”“3”“1/x”“=”得出結果3.

代數

數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算，字元代表未知數或未定數。如果不包括除法 (用整數除除外)，則每一個表達式都是一個含有理係數的多項式。例如： 1/2 xy+1/4z-3x+2/3. 一個代數方程式 (參見EQUATION)是通過使多項式等於零來表示對變數所加的條件。如果只有一個變數，那么滿足這一方程式的將是一定數量的實數或複數——它的根。一個代數數是某一方程式的根。代數數的理論——伽羅瓦理論是數學中最令人滿意的分支之一。建立這個理論的伽羅瓦(Evariste Galois，1811-32)在21歲時死於決鬥中。他證明了不可能有解五次方程的代數公式。用他的方法也證明了用直尺和圓規不能解決某些著名的幾何問題(立方加倍，三等分一個角)。多於一個變數的代數方程理論屬於代數幾何學，抽象代數學處理廣義的數學結構，它們與算術運算有類似之處。參見，如： 布爾代數(BOOLEAN ALGEBRA);群 (GRO-UPS);矩陣(MATRICES);四元數(QUA-TERNIONS );向量(VECTORS)。這些結構以公理 (見公理法 AXIOMATICMETHOD) 為特徵。特別重要的是結合律和交換律。代數方法使問題的求解簡化為符號表達式的操作，已滲入數學的各分支。