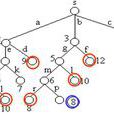
基本介紹
- 中文名:分支過程
- 外文名:branching process
- 類型:隨機過程
- 定義:數學模型
- 釋義:一種特殊的隨機過程
定義,離散時間分支過程,連續時間分支過程,
定義
分支過程是一種描述群體中個體數量的時齊馬爾可夫鏈。
離散時間分支過程
設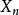 表示群體的第 n 代的個體總數,如果假定群體中每個個體之“子女”個數是獨立同分步的隨機變數,則
表示群體的第 n 代的個體總數,如果假定群體中每個個體之“子女”個數是獨立同分步的隨機變數,則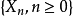 為[離散時間] 分支過程。以
為[離散時間] 分支過程。以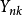 表示第 n 代中第 k 個個體的“子女”個數,於是
表示第 n 代中第 k 個個體的“子女”個數,於是
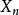
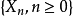
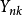
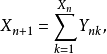
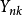
假定 Y 的母函式為 。可以證明
。可以證明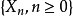 是時齊的馬爾可夫鏈,在
是時齊的馬爾可夫鏈,在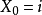 的假設下,
的假設下,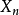 的母函式為
的母函式為

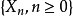
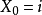
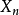
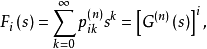
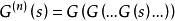
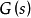
於是此鏈的轉移陣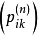 (從而有窮維分布)由
(從而有窮維分布)由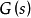 完全確定。如果群體中的個體數不能按“代”計算,而只能以
完全確定。如果群體中的個體數不能按“代”計算,而只能以 表示時刻 t 代個體總數,這時可考慮連續時間分支過程
表示時刻 t 代個體總數,這時可考慮連續時間分支過程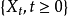 。
。
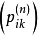
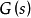

連續時間分支過程
設時間參數 t≥0 連續,b(t)Δt 表示在短時間 (t,t+Δt) 中發生一次分裂的機率,pk(t) 表示一個粒子分裂為 k 個的機率(k=0,1,2,…)。若 b(t) 、 pk(t) 連續,b(t)>0,則在時刻 t 的粒子數 Z(t) 構成一連續時間馬爾可夫鏈,於是可利用後者的理論來研究 {Z(t)} 。若 b(t),pk(t) 不依賴於 t ,則 {Z(t)} 是齊次的馬爾可夫鏈,這時可以得到許多類似於對 G-W 過程所得到的結果。