基本介紹
- 中文名:冪零矩陣
- 外文名:Nilpotent matrix
- 別稱:冪零陣、冪零方陣
- 表達式:N^k=0
- 套用學科:線性代數
- 屬性:收斂矩陣的一種特殊情況
簡介
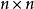


性質





舉例






分類



附加屬性



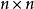



















線上性代數中,對於n階方陣N,存在正整數k,使得N^k=0,這樣的方陣N就叫做冪零矩陣。滿足條件的最小的正整數k被稱為N的度數或指數。更一般來說,零權變換是向量...
零矩陣,在數學中,特別是線上性代數中,零矩陣即所有元素皆為0的矩陣。在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及...
冪零變換是代數學名詞,指一類特殊的線性變換。線性代數的重要概念之一。設σ是數域P上的線性空間V的一個變換。若對於V中的任意向量α,β與P中的任意數k,有σ...
半單矩陣(semisimple matrix)是一種特殊矩陣,指最小多項式無重根的矩陣。各種特殊的矩陣除半單矩陣外還有三角矩陣、冪零矩陣、冪等矩陣和冪麼矩陣等。半單矩陣...
冪零李代數(nilpotent Lie algebra)類似於一般代數中的冪零代數。若L為域F上...在此運算下,L為李代數.特別地,若L為由所有n×n矩陣構成的結合代數,則在矩陣...
這兩個矩陣是可交換的,因為其中一個是對角矩陣。不僅如此,矩陣N是一個冪零矩陣。因此,每個相似於若爾當標準型的矩陣都可以寫成可交換的一個對角矩陣和一個冪零...
式中,𝑬為奇異矩陣。上述奇異微分方程有唯一解的充分必要務件是(s𝑬-𝑨) 為正則束。在此條件下,該系統可等價地化成其中,𝑵為冪零矩陣。與正常系統不同...
2.8.4 冪等矩陣 2.8.5 冪零矩陣 2.8.6 對合矩陣 2.8.7 正交矩陣 習題2 第3章 線性方程組 3.1 Cramer法則 3.2 齊次線性方程組 3.2.1 齊次線性方程組有...
§3 冪零矩陣的標準形式§4 若爾當標準形式索引參考資料 1. 高等代數第五版 .京東[引用日期2017-11-08] 詞條標籤: 出版物 , 書籍 圖集 高等代數第五版圖冊...
在這方面最早的一篇論文是《關於冪零矩陣的復型的一個註記》。在這篇論文中,段學復對前述謝瓦萊的第一篇文章里的定理6,給出了一個利用矩陣若爾當(Jordan)標準...
8.7 矩陣方冪的若干求法一、秩為1的情況二、可分解為數量矩陣和冪零矩陣之和的情況三、歸納法(實例)四、利用相似變換法五、特徵多項式法(或最小多項式法)...
7.3 冪等矩陣與對合矩陣7.4 冪零矩陣7.5 循環矩陣習題七第八講 矩陣分解8.1 矩陣的秩分解8.2 矩陣的滿秩分解8.3 矩陣的LU分解...
21.中心對稱矩陣 22.用逆矩陣求不定積分 23.根子空間分解及其直接求法 24.冪零矩陣 25.用若爾當鏈求若爾當標準形及變換矩陣 26.友矩陣與范德蒙德矩陣 27.線...
附錄 向量空間的分解和矩陣的若爾當標準形式知識結構圖§1 向量空間的準素分解凱萊-哈密頓定理§2 線性變換的若爾當分解§3 冪零矩陣的標準形式...
A.4冪零矩陣 A.5線性空間的一些運算 A.6矩陣的核空間和象空間 A.7奇異值分解 附錄B秩約束下的矩陣匹配和最小二乘問題 B.1問題的描述 B.2準備工...
