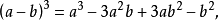公式分解法

公式分解法(factoring with multiple formula)是多項式分解因式的一種方法，它是乘法公式的逆向套用，即利用乘法公式把多項式進行因式分解的方法。套用此法的主要技巧是將給定的多項式中的一些式子視為乘法公式的一項，使公式得以套用。例如利用乘法公式a³+b³=(a+b)(a²-ab+b²)將多項式8x³+27y⁶在有理數集上分解：8x³+27y⁶=(2x)³+(3y²)³=(2x+3y²)(4x²-6xy²+9y⁴)。另外，此法常與分組分解法結合起來使用。分解因式常用的公為多項式的乘法公式。

基本介紹

• 中文名：公式分解法
• 外文名：factoring with multiple formula
• 所屬學科：數學
• 所屬問題：初等代數(代數式)
• 簡介：多項式分解因式的一種方法，

平方差的因式分解公式

多項式a²-b²可以分解成兩個因式，就是

事實上，這裡我們是反過來套用了兩數和與差的積的公式。

我們可以把(1)作為一個公式，利用它來分解由一個數的平方減去另一個數的平方所構成的多項式的因式。

平方差的因式分解公式:

(因式分解公式1)

完全平方的因式分解公式

我們計算兩數和或差的平方時可以套用下面的公式:

反過來就得到完全平方的因式分解公式:

(因式分解公式2)，

(因式分解公式3)。

注 因為和可以分別化成兩個數的和或者兩個數的差的平方，我們把它們叫做完全平方式。

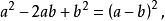
立方和或立方差的因式分解法

從乘法公式:

及

反過來就得到立方和或立方差的因式分解公式:

(因式分解公式4)，

(因式分解公式5)。

完全立方的因式分解法

從乘法公式:

及

反過來可得完全立方的因式分解公式，

(因式分解公式6)，

(因式分解公式7)。