設Ω是C中的域,如果對任意K⊂Ω,從K⊂⊂Ω能推出Ǩ⊂⊂Ω,就稱Ω是全純凸域。
基本介紹
- 中文名:全純凸域
- 外文名:domain of holomorphically convex
- 適用範圍:數理科學
簡介
全純凸包

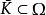

全純凸域
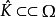
全純域

設Ω是C中的域,如果對任意K⊂Ω,從K⊂⊂Ω能推出Ǩ⊂⊂Ω,就稱Ω是全純凸域。

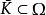

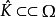

設Ω是C中的域,如果對任意K⊂Ω,從K⊂⊂Ω能推出Ǩ⊂⊂Ω,就稱Ω是全純凸域。...
全純域是刻畫自然邊界的域。C中的域Ω稱為全純域,如果不存在比Ω更大的域Ω′(Ω′⊃Ω,Ω′≠Ω),使得Ω上全部全純函式都能全純地開拓到Ω′上去。復...
(2) 建立了中有界凸平衡域上的雙全純凸映照的一個充要條件和無窮維Hilbert空間中的單位球上的雙全純凸映照的一個充要條件,解決了Graham 和Kohr提出的一個...
施坦流形是從多複變函數論角度研究最多的複流形,它是全純凸域在複流形上的推廣。...... 施坦流形是從多複變函數論角度研究最多的複流形,它是全純凸域在...
G.)定理和外爾斯特拉斯定理在多復變中的推廣的兩個問題和列維提出的擬凸域是否全純域的問題更是長期以來推動著多複變函數論的發展。...
他們的研究揭示了多復變全純函式本質上的獨特性。在這當中,庫辛提出的關於全純函式整體性質的兩個以他命名的問題以及E.E.列維提出的擬凸域和全純域是否等價的...
第三類典型域(classical domain of third class)是典型域之一。典型域是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的標準域稱為典型域。...
第一類典型域(classical domain of first class)是典型域之一。典型域是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的標準域稱為典型域。...
第一章 全純域與全純凸域 1.1 全純域 1.2 全純凸域 第二章 擬凸域 2.1 擬凸域 2.2 多次調和函式 第三章 L2估計 3.1 L2方法 3.2 ...
第二類典型域(classical domain of second class)是典型域之一。典型域是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的標準域稱為典型域...
列維問題(Levi problem)是關於擬凸域和全純域是否等價的問題。根據嘉當一蘇倫定理,不難證明全純域是擬凸域。困難的、長期未決的是其反面:擬凸域是否一定是全純...
嘉當一蘇倫定理(Cartan-Thullen theorem)用全純凸刻畫全純域的重要定理.嘉當一蘇倫定理斷言:全純域和全純凸域是等價的.這是刻畫全純域的特徵的第一個重要結果...
偽凸域(191)14. 全純包40. 單葉包(197) 41. 多葉包(202) 42. 奇點集的解析性(207)問題第iv章 亞純函式和留數15. 亞純函式...
偽凸域(191)14. 全純包40. 單葉包(197) 41. 多葉包(202) 42. 奇點集的解析性(207)問題第iv章 亞純函式和留數15. 亞純函式...
12.全純域33.全純域的概念34.全純凸35.全純域的性質13.偽凸域36.連續性原理37.局部偽凸性38.多重次調和函式39.偽凸域14.全純包...
第四類典型域(classical domain of fourthclass)亦稱李球,典型域之一。典型域是多複變函數論的基本概念。Cn中不可分解對稱有界域在全純等價下分類的標準域稱為...
嘉當-蘇倫定理是用全純凸刻畫全純域的重要定理。嘉當-蘇倫定理斷言:全純域和全純凸域是等價的,這是刻畫全純域的特徵的第一個重要結果。...
