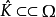嘉當-蘇倫定理

嘉當-蘇倫定理是用全純凸刻畫全純域的重要定理。嘉當-蘇倫定理斷言：全純域和全純凸域是等價的，這是刻畫全純域的特徵的第一個重要結果。

基本介紹

• 中文名：嘉當-蘇倫定理
• 外文名：Carten-Thullen theorem
• 適用範圍：數理科學

簡介

嘉當-蘇倫定理是用全純凸刻畫全純域的重要定理。

嘉當-蘇倫定理斷言：全純域和全純凸域是等價的，這是刻畫全純域的特徵的第一個重要結果。

全純域

全純域是刻畫自然邊界的域。C中的域Ω稱為全純域，如果不存在比Ω更大的域Ω′(Ω′⊃Ω，Ω′≠Ω)，使得Ω上全部全純函式都能全純地開拓到Ω′上去。複平面C上的域都是全純域，但當n>1時，C中確實存在著非全純的域。例如：

就是非全純域。這是多復變數函式論和單復變數函式論的一個本質差異之處。

全純凸域

設Ω是C中的域，K是Ω的一個子集，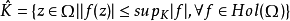

稱為K在Ω中的全純凸包，其中Hol(Ω)表示Ω上全體全純函式構成的集合。如果且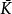是緊的，則稱Ω的子集K相對於Ω是緊的，記為K⊂⊂Ω。

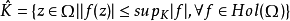
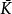
設Ω是Cⁿ中的域，如果對任意K⊂Ω，從K⊂⊂Ω能推出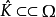，就稱Ω是全純凸域。