克里斯托費爾符號是黎曼聯絡的聯絡係數,且不是張量,有第一類克里斯托費爾符號和第二類克里斯托費爾符號。
基本介紹
- 中文名:克里斯托費爾符號
- 外文名:Christoffel symbols
- 所屬學科:數學
- 分類:第一類和第二類克里斯托費爾符號
- 相關概念:黎曼聯絡、張量等
定義


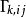




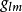





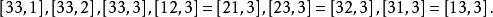

用克里斯托費爾符號表示基本張量的導數








克里斯托費爾符號的變換率







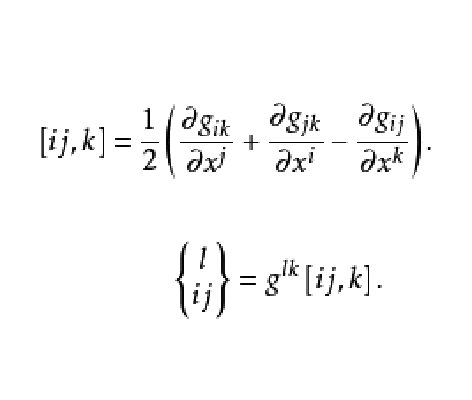
克里斯托費爾符號是黎曼聯絡的聯絡係數,且不是張量,有第一類克里斯托費爾符號和第二類克里斯托費爾符號。


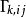




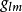





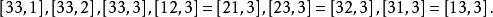
















克里斯托費爾符號是黎曼聯絡的聯絡係數,且不是張量,有第一類克里斯托費爾符號和第二類克里斯托費爾符號。...
瑞士數學家,他還引進了第一類克里斯托費爾符號 及第二類克里斯托費爾符號這些工作成為後來張量演算的基礎。...
克里斯托費爾(Christoffel,Elwin Bruno,1829~1900),瑞士數學家。生於亞琛附近的蒙茹瓦(今蒙紹),1900年3月15日卒於斯拉斯堡。1850~1854年到柏林大學學習,1856年獲...
在直角坐標系下,協變和逆變間的差別消失,故可規定所有指標均寫成下標,另外,由於克里斯托費爾符號為零,所以協變導數變成為普通偏導數。 [1] ...
克里斯托費爾符號表示基本張量的導數克里斯托費爾符號的變換律張量分析矢量協變微分 編輯 基矢量的協變導數逆變矢量的協變導數協變矢量的協變導數...
克羅內克符號δ 張量的基本運算 對稱張量和反對稱張量 矩陣 線元和度量張量 相伴張量 克里斯托費爾符號 測地線 協變導數 張量形式的梯度、散度和旋度 ...
§3.2 正交曲線坐標系的克里斯托費爾符號 §3.3 矢量的協變導數 §3.4 高階張量的協變導數 §3.5 張量方程 §3.6 梯度、散度、旋度 §3.8 黎曼-克里斯托費爾...
係數Γi j稱為克里斯托費爾符號。 然後使用定義中的規則,我們發現對於一般的向量場 可以得到這個公式的第一項代表了坐標系對於共變導數的"扭轉",而第二項代表了...
逆變矢量、協變矢量和張量克羅內克符號δ張量的基本運算對稱張量和反對稱張量矩陣線元和度量張量相伴張量克里斯托費爾符號測地線協變導數張量形式的梯度、散度和旋度...
是度量的克里斯托費爾符號。不像黎曼曲率張量或里奇張量可以對任何仿射聯絡自然地定義,數量曲率只在黎曼幾何存在;其定義與度量密不可分。 [1] 里奇...
其中 表示第二類克里斯托費爾符號, 則表示黎曼-克里斯托費爾曲率張量。[2] 參考資料 1. 楊桂通.彈性力學:高等教育出版社,2011 2. C Amrouche, PG Ciarlet, L ...
克里斯托費爾(Christoffel,E.B.)於1869年創立了用度量張量gij的微商構造的克里斯托費爾符號。後來,里奇(Ricci,C.G.)將克里斯托費爾的方法做了系統的闡述和發展,...
中,拉普拉斯–貝爾特拉米運算元利用度量張量與克里斯托費爾符號可表示如下:注意到通過使用球坐標與圓柱坐標的度量張量,我們類似地可重新得到拉普拉斯運算元在球坐標與圓柱坐標...
5.1克里斯托費爾符號79 5.2矢量的協變微分79 5.3張量的協變微分80 5.4協變微分法規則80 5.5不變微分運算元80 5.6內稟微分81 5.7相對張量81 習題演算82第...
聯絡形式沒有張量性因為在基變化下,聯絡形式的變換涉及到轉移函式的外微分,與列維-奇維塔聯絡的克里斯托費爾符號非常類似。一個聯絡形式的主要張量性不變數是其曲率...
在黎曼流形和偽黎曼流形的理論中,共變導數一詞經常用於列維-奇維塔聯絡。聯絡的坐標空間的表達式稱為克里斯托費爾符號。 [1] 列維-奇維塔聯絡黎曼幾何 編輯 ...
5 曲面論的基本定理5.1 曲面的基本方程和克里斯托費爾符號5.2 曲面的黎曼曲率張量和高斯-科達齊-邁因納爾迪公式5.3 曲面論的基本定理習題2.56 曲面上的測地線...
這裡是第二類克里斯托費爾符號,射影變換下最重要的不變張量是下式定義的射影曲率張量式中,Rij分別是M的曲率張量和里奇曲率張量。一個黎曼流形的最大射影變換群...
數量曲率 里奇流 克里斯托費爾符號 參考資料 1. Princeton University Press. Blow-up Theory for Elliptic PDEs in Riemannian Geometry (MN-45):[J]. 2004...
