基本介紹
- 中文名:克羅內克爾符號
- 外文名:Kronecker symbol
- 所屬學科:數學
- 符號表示:δij
- 相關概念:愛因斯坦求和符號等
定義
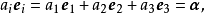
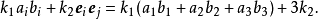




相關性質


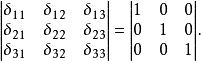
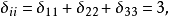
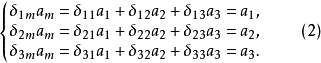

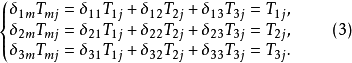
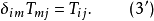

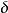
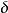
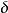


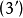


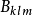

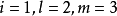
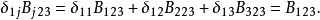

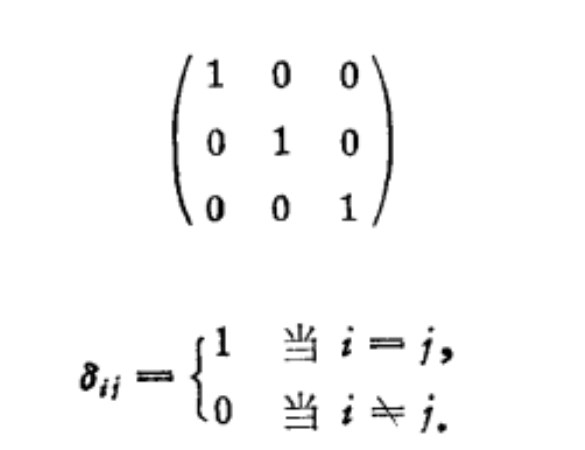
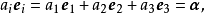
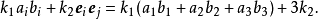






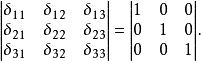
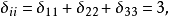
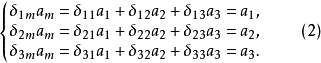

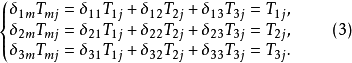
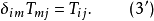

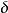
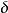
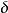


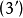


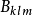

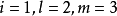
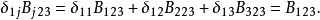

設I為集合,I×I的對角線的特徵函式稱為克羅內克爾符號(Kronecker symbol),並記為δ。習慣上將這個映射視為通過集合I×I確定下標的族;於是:如果i≠j,δij=0;...
克羅內克函式的值一般簡寫為 。克羅內克函式和狄拉克δ函式都使用δ作為符號,但是克羅內克δ用的時候帶兩個下標,而狄拉克δ函式則只有一個變數。...
克羅內克函式的值一般簡寫為 。克羅內克函式和狄拉克δ函式都使用δ作為符號,但是克羅內克δ用的時候帶兩個下標,而狄拉克δ函式則只有一個變數。 [1] ...
Kronecker delta,即克羅內克函式(又稱克羅內克δ函式、克羅內克δ、克羅內克符號)δij是一個二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(...
這裡就是克羅內克爾δ。當 = ,,否則就是0。邏輯上,可以把方程式中的i轉為j或者把j轉為i。叉積這裡的 。是Levi-Civita 符號。它的定義:...
克羅內克函式的自變數(輸入值)一般是兩個整數,如果兩者相等,則其輸出值為1,否則為0。克羅內克函式的值一般簡寫為 。克羅內克函式和狄拉克δ函式都使用δ作為符號,...
也可以寫作克羅內克爾δ記法:矩陣單位克羅內克函式 編輯 在數學中,克羅內克函式(...克羅內克函式和狄拉克δ函式都使用δ作為符號,但是克羅內克δ用的時候帶兩個下標...
A.1指標符號A.2克羅內克爾符號δijA.3矢量A.4張量附錄B非線性有限元模擬技術簡介B.1有限單元法簡述B.2有限元法分析過程B.3非線性有限單元法...
而克羅內克爾符號δ在四維時空下跡4,所以式子可寫作:是故R=0。因此可以得到此一更常見的方程 [1] :場方程宇宙常數不為零 若宇宙常數不為零,則方程為...
1.5變分法基本引理271.6求和約定、克羅內克爾符號和排列符號311.7張量的基本概念351.7.1直角坐標旋轉變換351.7.2笛卡兒二階張量361.7.3笛卡兒張量的代數運算38...
克羅內克爾符號和排列符號 1.7 張量的基本概念 1.7.1 直角坐標旋轉變換 1.7.2 笛卡兒二階張量 1.7.3 笛卡兒張量的代數運算 1.7.4 張量的商定律 1.7.5...
