基本介紹
- 中文名:光的折射定律
- 外文名:refraction law
- 表達式:n12=sinθ1/sinθ2
- 提出者:斯涅耳
- 提出時間:1621年
- 套用學科:光學
定律定義

數學推導
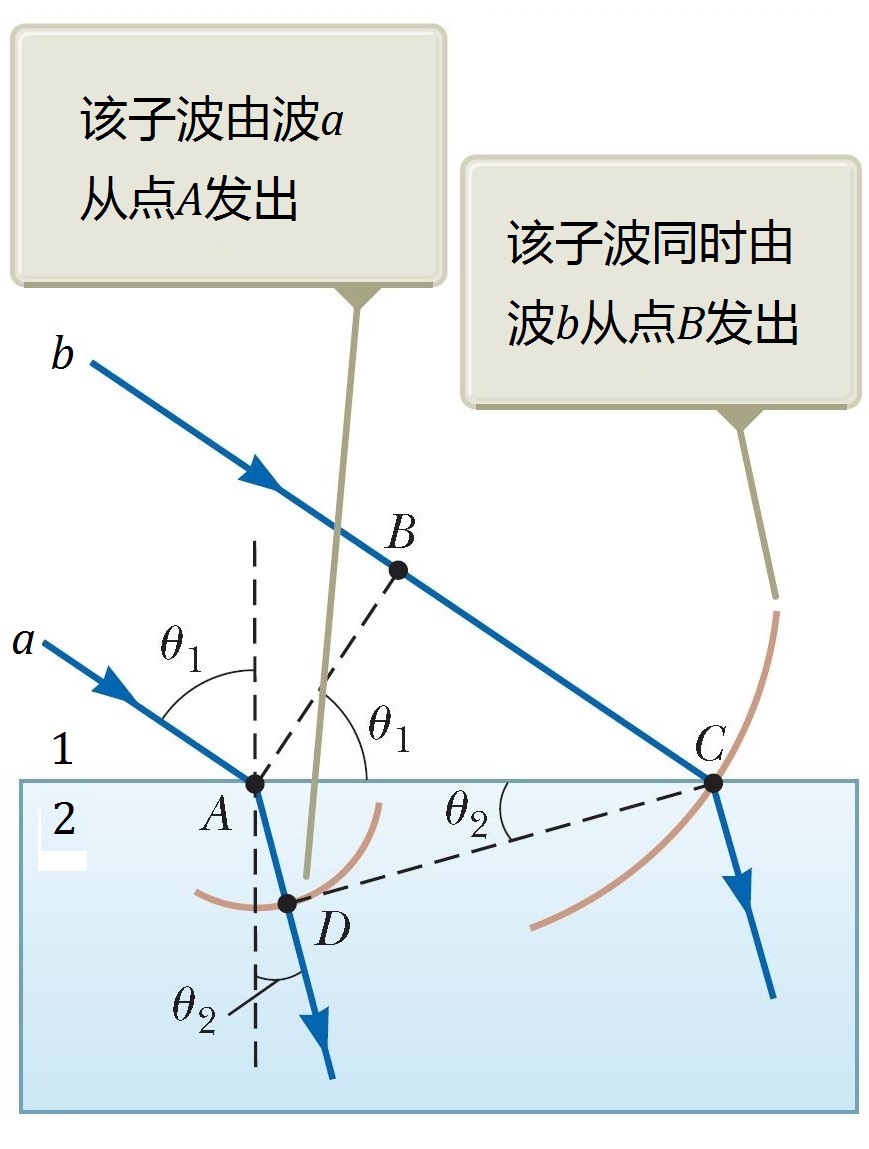











光的折射定律是幾何光學的基本定律之一。是在光的折射過程中,確定折射光線與入射光線之間關係的定律。1621年由斯涅耳提出。光從一種介質射向另一種介質的平滑界面...
光從一種介質斜射入另一種介質時,傳播方向發生改變,從而使光線在不同介質的交界處發生偏折。(光在真空中偏折角度最大)特性:光的折射與光的反射一樣都是發生在...
光的折射:光從一種透明介質斜射入另一種透明介質時,傳播方向一般會發生變化,這種現象叫光的折射。理解:光的折射與光的反射一樣都是發生在兩種介質的交界處,只是...
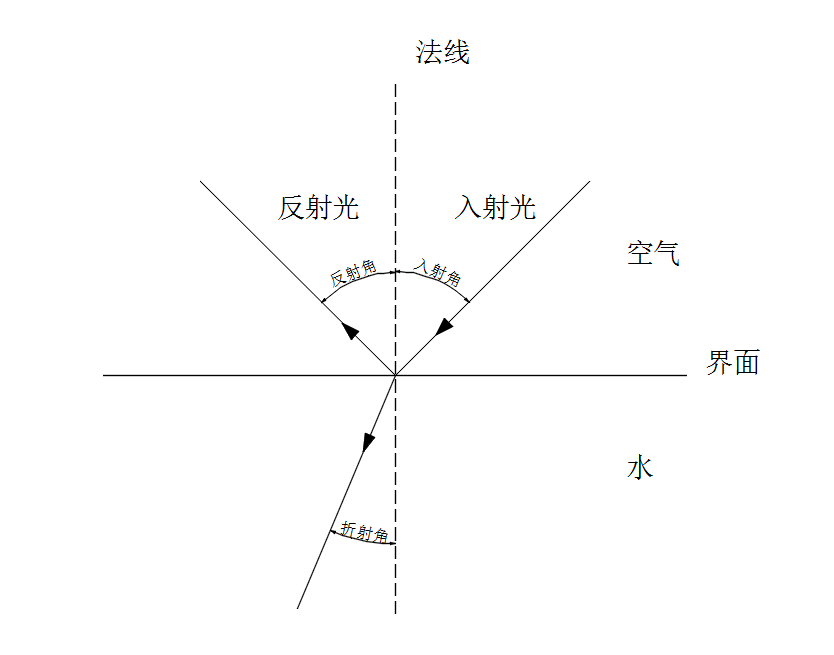
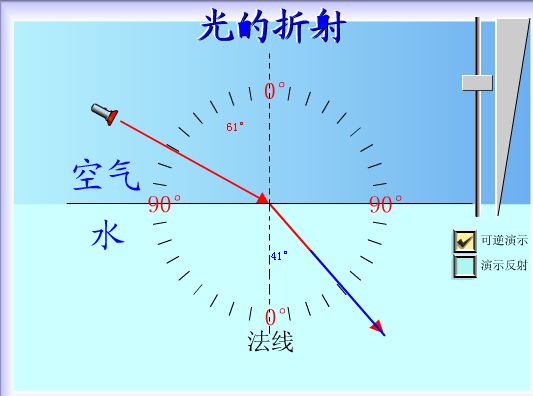
折射光線與法線的夾角叫折射角。其折射情況遵循折射定律。光從空氣斜射入水或其他介質中時,折射角小於入射角,當入射角增加時,折射角隨著增加。光從水中或其他介質...
折射現象是指當光由一種介質(比如水)斜射入第二介質(比如空氣)時,在界面上部份光發生偏離原來路線而與原來路線產生夾角的現象。...
光線通過兩介質的界面折射時,確定入射光線與折射光線傳播方向間關係的定律,幾何光學基本定律之一。如圖,入射光線與通過入射點的界面法線所構成的平面稱為入射面,...
斯涅爾定律(Snell's Law)因荷蘭物理學家威理博·斯涅爾而命名,是一條描述光的折射規律的定律,即:光入射到不同介質的界面上會發生反射和折射。在物理學的光學中...
球面折射的規律是多數光學鏡頭設計中的基本規律,因為許多複雜的光學鏡頭,都由一系列球面組成的。中文名 球面折射 外文名 Spherical refraction 學科 光學 領域 ...
通過以上運算我們看到:用“光和物質間相互作用力理論”,計算光折射的數據比用“光的折射定律”計算的更準確。不論在巨觀領域觀測或是在微觀領域觀察;不論是在光...
威里布里德.斯涅耳(Willebrord Snell Van Roijen 1580-1626),荷蘭萊頓人,數學家和物理學家,曾在萊頓大學擔任過數學教授。斯涅爾最早發現了光的折射定律,從而使幾何...
光現象折射規律 簡記為:三線共面,一邊一個,兩角不等。光從空氣斜射入水中或其他介質中時,折射光線向法線方向偏折;當光從水中斜射入空氣中時,折射光線向界面方向...
在均勻介質中,光線直線傳播 光的反射定律 光的折射定律 光程可逆性原理 由於光本身就是從原子、分子內發出的高頻電磁場,因此上述原理都可以通過電動力學中...
光的折射定律(斯涅爾定律)。最短光時線可以有多條,例如光線從橢圓面焦點A經過反射到另一焦點B,可以有無數條路徑,所有這些路徑的光線傳播時間都相等。[1] 費馬...
1 簡介 2 入射光線 3 分類 ▪ 反射光線 ▪ 折射光線 ▪ 定義 ▪ 光的折射定律 出射光線簡介 編輯 入射光線經物體反射或者折射後射出的光線,叫...
光程(optical path)是光學領域的一個基礎概念,其定義為光傳播的幾何路程與介質折射率的乘積。光程差(optical path difference)顧名思義,即為兩束光光程之差,在...
他將這一機械問題,通過已有的費馬最小時間原理的分析轉化為光學問題,從光的折射定律推出了旋輪線的微分方程.雅格布從另一個角度給出了一個較麻煩但更一般的解法...
這一實驗結果與波動說相一致而與牛頓的微粒說相矛盾(解釋光的折射定律時),這對光的波動本性的確立在歷史上曾起過重要作用。1851年,菲佐用干涉法測量了運動介質...
