光在分界面上的折射和反射,當光通過兩種透明媒質分界面時,入射光分為反射光與折射光。
基本介紹
- 中文名:光在分界面上的折射和反射
- 學科:物理
基本信息
特點
設圖1的a和b中A、B為兩種不同的透明媒質,它們對真空的折射率分別為與。兩者的交界面為垂直軸的=0平面。如此軸為該平面的法線,為入射面(也稱投射面)。當自然光入射到分界面時,由於自然光可分解為相互垂直並且相互獨立的兩個大小相等的平面偏振光,所以可把垂直入射面與平行入射面的電矢量分開來討論。以s表示垂直入射面,p表示平行入射面,則分別表示垂直入射面與平行入射面偏振的入射光、反射光姈和透射光的電矢量。又根據電磁波中與方向的規定,即垂直,給出了磁矢量的方向。圖中箭頭表示各矢量在給定的方向時的正方向。對垂直矢量,以為正方向, 即以⊙表示從入射面出來,指各該矢量的正方向。現在先分析電矢量垂直入射面的圖1a,在那裡磁矢量是平行入射面的。根據電磁理論的邊界條件:平行邊界的電磁場是連續的,即邊界這邊的等於邊界另一邊的,於是可導出偏振垂直入射面的反射光和折射光與入射光的振幅比,分別為
 光在分界面上的折射和反射
光在分界面上的折射和反射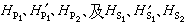 光在分界面上的折射和反射
光在分界面上的折射和反射(2)
再同樣分析電矢量平行入射面的偏振,得反射光和折射光與入射光的振幅比,分別為這四個公式稱菲涅耳公式。
 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射(4)
這四個公式稱菲涅耳公式。
光在分界面上的折射和反射光在分界面上的折射和反射以玻璃平面上的反射為例。設該玻璃對空氣的折射率=/=1.50,在不同的入射角,從菲涅耳公式,得到兩個不同偏振的反射光、折射光與入射光振幅的比,如圖2所示。實驗證明它們的關係是正確的。現在來討論幾個特殊情況。
半波損失 分兩種情況:
①對上例入射角為零時兩種偏振的反射光振幅與入射光振幅的比值都是(-1)/(+1)=0.2,但平行入射面的偏振為正而垂直入射面的偏振為負。按圖1所示的方向,表示反射光的電矢量都有的位相躍變,即所謂從光疏到光密媒質反射時有半波損失。反射與入射的光強比對兩種偏振都一樣。即。故一個玻璃面,在垂直入射光照射下能反射 4%的入射光。因而在光學透鏡表面上需要塗鍍增透膜以減少反射。這門科學稱薄膜光學。它的基礎是菲涅耳公式。
②上面已提出在=0時平行入射面的偏振,反射光與入射光的電矢量之間有相差。菲涅耳公式還指出,在小於偏化角時為正,等於偏化角時為0,大於偏化角時為負。負表示的方向與圖1所指的方向相反,即和捓的位相經過大於的反射改變了。至於是始終相反的。從這個結果,可以推出:光從光疏到光密(>)媒質進行折射時,在垂直入射(≈0)及掠射時(≈90°),在媒質面上,入射光與反射光的電矢量,不論偏振垂直入射面或平行入射面,都取相反振動方向,分別如圖3所示。這就是所謂從光疏到光密媒質反射時的半波損失。
光在分界面上的折射和反射偏化角 從圖2或式(3),當=0,反射光中沒有平行入射面的偏振光,只有垂直入射面的偏振光。由於sin/sin=,此時=,得==tg。對於=1.50的玻璃,=57°。這個角稱為偏化角,亦稱布儒斯特角,是D.布儒斯特在1815年發現的。
因此在媒質面上利用偏化角反射是獲得偏振光最簡單的方法。但在透射光中還有偏振垂直入射面的成分,故透射光為部分偏振光。需要經過多次反射,如雷射器共振腔的一端或二端,按布儒斯特角放置平行窗片,經窗片多次來回反射可獲得偏振平行入射面的偏振光。
內反射 上面討論的從光疏媒質到光密媒質的反射稱外反射。下面討論從光密到光疏媒質的反射,稱內反射。仍採用為入射角,為折射角,但>,/=1/,仍保持>1,菲涅耳公式仍適用。此時偏化角,全反射極限角。當>,>90°,光全反射。
在外反射中所討論的二偏振光的反射光與入射光的位相差與,可得位相差的差墹
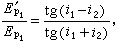 光在分界面上的折射和反射
光在分界面上的折射和反射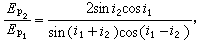 光在分界面上的折射和反射
光在分界面上的折射和反射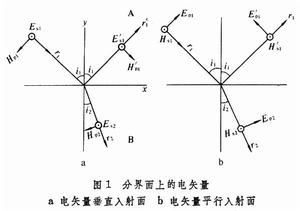 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射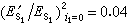 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射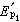 光在分界面上的折射和反射
光在分界面上的折射和反射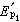 光在分界面上的折射和反射
光在分界面上的折射和反射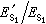 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射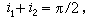 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射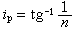 光在分界面上的折射和反射
光在分界面上的折射和反射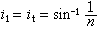 光在分界面上的折射和反射
光在分界面上的折射和反射墹=π,
當i1>ip。
圖4a表示外反射中的墹與的關係。但在內反射中情況並非如此簡單,根據計算
。 (6)
它們二者位相差墹為
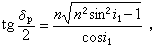 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射光在分界面上的折射和反射光在分界面上的折射和反射
 光在分界面上的折射和反射
光在分界面上的折射和反射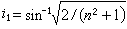 光在分界面上的折射和反射
光在分界面上的折射和反射 光在分界面上的折射和反射
光在分界面上的折射和反射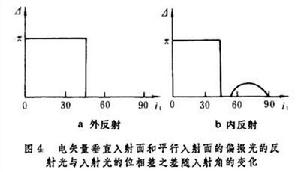 光在分界面上的折射和反射
光在分界面上的折射和反射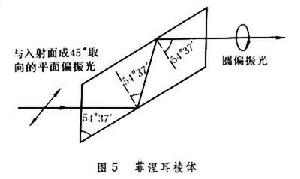 光在分界面上的折射和反射
光在分界面上的折射和反射