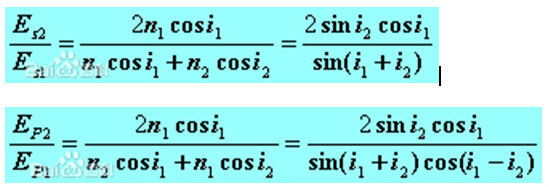歷史背景
菲涅耳公式的形成
光波通過不同介質的分界面時會發生反射和折射,入射光分為反射光和折射光兩部分。這兩束光的進行方向之間的關係雖可由反射和折射定律決定,但二光束的振幅和振動取向卻不能決定。菲涅耳以光是橫波的構想為基礎,把入射光分為振動平面平行於入射面的線偏振光和垂直於入射面的線偏振光,並導出了光的折射比、反射比之間關係的菲涅耳公式。由菲涅耳公式可以求出一定入射角下反射和透射的振幅、強度等。可以很好地解釋光的反射與折射的起偏問題及半波損失問題等。菲涅耳公式作為光學和電磁理論的一個重要基本公式。而且在薄膜及電磁現象中套用非常廣泛。
公式定義
當光通過不同的介質界面時,入射光分為反射光和折射光兩部分,折射定律和反射定律決定了他們的方向,
而這兩部分光的強度和振動的取向,都需要用電磁理論中的“菲涅耳公式”來解釋,把這種理論稱為“菲涅耳公式”。
公式推導
菲涅耳公式是由電磁場邊值關係出發的理論推演得出的,其間先後引用了若干條件,因此菲涅耳公式也有其成立條件。
滿足電磁場邊值關係
 菲涅耳公式的導出
菲涅耳公式的導出電磁場的運動變化規律由麥克斯韋方程組所反映,將麥克斯韋積分方程套用於兩介質界面處就得到了電磁場邊值關係,在巨觀電磁理論看來,經過界面,介質的電磁性能參數有了突變,從而使得電磁場一般地也發生突變.電磁場邊值關係反映了這種場突變的規律.電磁場邊位關係有四條如圖:
下標n,t分別代表法向和切向的分量,D,B分別是電位移和磁感應強度。
由於在界面(z=0)上波函式中的指數因子都一樣可略去不 寫。上面的邊值關係可寫成如下分量形式,結合右圖:
Fresnel公式推導中光的局域坐標系正方向是隨便取定的,不同書有不同書的取法。尤其是入射光和出射光的正方向如果不同,體現在公式上會有正負號的差別。所以在用公式時要注意書中的規定。一般來說只要求正號是平行,負號是反平行。
Fresnel equations中的坐標系取的便是方向規定為的坐標系。

公式關係
反射、折射瞬間的電矢量與入射電矢量之間的關係。
反射光
折射光
注意事項
應當注意各分量量值之比是相對於入射波來計算的,但振動方向則分別按照各波的上述規定,不是直接相對於入射波作比較(s分量還可比較,p分量則無法簡單地用正負號來直接表示出各波之間的振動方向關係).
對通常的入射光波來說,As1和Ap1兩分量的振動方向都可認為是正的,量值可認為彼此相等.這是因為對於通常的熱光源所發的光,在垂直於傳播方向的平面(波面)內電矢量(以及磁矢量)可以在任何方向振動,這些振動中的每一個矢量都在毫無規則地非常迅速地改變著.我們觀察到的僅是它們的平均位值.因而我們可以運用標量近似處理來代替矢量波.在隨意選定了任何兩個互相垂直的方向(例如s和p兩個方向)之後,就可以把任一振動的振幅A沿所取的方向分成和兩個分量.在平均效應中沒有任何特殊理由必須認為那一個是正,那一個是負,因而通常就認為它們都是正的.這兩個分振動的平均能量為。

得出結論
既然入射光諸振動分量都看作是正的,所以菲涅耳公式中的符號,可以認為只是對反射和折射光而言的,反射光和折射光都是在入射點突然改變傳播方向的,因此,一般地說,電矢量也將在這裡突然改變方向。
實驗分析
實驗過程
現在用菲涅耳公式來解釋半波損失問題。在洛埃鏡實驗中,光從空氣入射到玻璃,即。按折射定律,知道。由於,,令入射光中的As1,Ap1均取正值,所以;。
從圖中可以看到,在i1=90°的掠射情況下,入射光和反射光的傳播方向幾乎相同,它們的波面I和II幾乎相互平行.此時,對Ap1′和Ap1規定的正方向也幾乎相同,由於在無限靠近界面處反射光中電矢量的兩個分量都取負值,而且滿足,它們的合矢量幾乎與這裡入射光中的合矢量方向相反.在波的航進路程上,通常是每隔半個波長,振動矢量的方向相反.現在則是在同一地點(界面上的入射點),而不是相隔半個波長處,僅是由於反射過程,振動方向就變成相反了.所以稱為半波損失(這是對電矢量說的,根據E、H和傳播方向三者之間所構成的右螺旋關係可知,磁矢量在這情況中,也同樣產生半波損失)。
在維納駐波實驗中,i1幾乎等於零.仍設n1i2,得As1′0.但按照各自規定的正方向,反射光中的As1′和Ap1′都分別與入射光中的As1和Ap1反向,而且滿足,這就是說合矢量反向.這也是在同一地點(入射點)而不是相隔半個波處,僅僅是由於反射過程使振動方向變成相反.所以在這情況中(i1≈0)也發生了半波損失.這也是對電矢量說的.由於這裡反射光和入射光的傳播方向是相反的,所以磁矢量的方向不變,不產生半波損失.因此,介質表面對駐波中的電矢量來說是波節,但對磁矢量來說仍應該是波腹.維納實驗所用感光乳膠在介質表面上不感光表示對感光作用說,電矢量是主要的.此處磁矢量雖是波腹,但乳膠並不感光,說明磁矢量對感光不起作用.這一結果是容易解釋的,因為電磁波的磁矢量作用在電子上的洛侖茲力qvB比電矢量的作用力qE小得多,其比值為v2/c2,式中v和c分別為電子的速度和光速,一般可以略去不計。
實驗總結
總結洛埃鏡實驗和維納實驗,可得這樣的結論:入射光在光疏介質(n1小)中前進,遇到光密介質(n2大)的界面時,在掠射(i1≈90°)或正射(i1≈0)兩種情況下,反射光的振動方向對於入射光的振動方向都幾乎相反,都將在反射過程中產生半波損失,這是僅對電矢量而言的.在光的效應中,一般僅考慮電矢量的作用.正是這個原因,我們常把電場矢量稱為光矢量,電場稱為光場.入射光在光密介質中前進,遇到光疏介質的界面而反射時(n1>n2),不產生半波損失。
由上可知,不論在掠射或正射時,相對於入射光的振動方向,折射光的振動方向永遠不發生半波損失。
 菲涅耳公式的導出
菲涅耳公式的導出

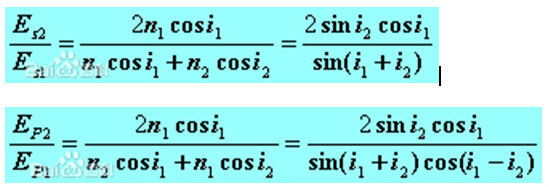


 菲涅耳公式的導出
菲涅耳公式的導出