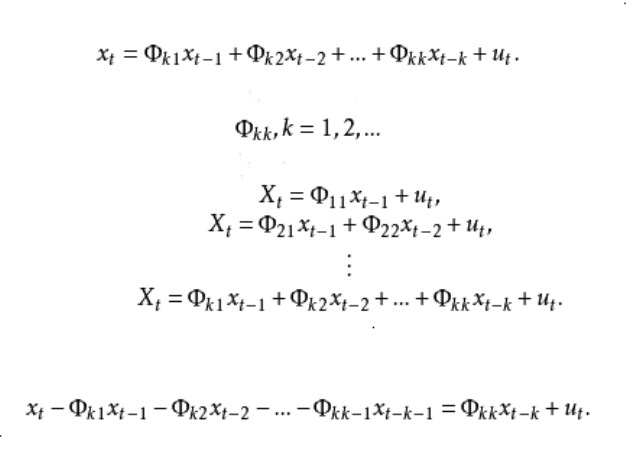偏自相關函式的定義
用Φk1xt-1+Φk2xt-2+...+Φkkxt-k+ut,表示k階自回歸式中第j個回歸係數,則k階自回歸模型表示為
因自相關函式中每一個回歸係數
恰好表示
與
在排除了其中間變數
影響後的自相關係數,即
偏自相關函式求解
將k=1,2,...代人上式連續求解、可求得偏自相關函式
自回歸模型的偏自相關函式
對於AR(1)過程,當k=1時,
≠0;當k>1時,
=0,所以AR(1)過程的偏自相關函式特徵是在k=1時出現峰值(
=ρ
1),然後截尾,如圖1所示。
1
1>0)" style="float: none; display: block; margin: 0px auto; clear: both;" picsrc="ac345982b2b7d0a2756dda69c7ef76094a369a9a" data-layout="blockcenter" width="475" height="288" url="https://gss1.bdstatic.com/9vo3dSag_xI4khGkpoWK1HF6hhy/baike/s%3D220/sign=e1bb99ca00f3d7ca08f63874c21ebe3c/ac345982b2b7d0a2756dda69c7ef76094a369a9a.jpg" compressw="220" compressh="133" useredit="1" />

 圖1(b)AR(1)過程的偏自相關函式圖(φ11<0)
圖1(b)AR(1)過程的偏自相關函式圖(φ11<0)對於AR(2)過程,當k<2時,
≠0;當k>2時,
=0。偏自相關函式在滯後期2以後有截尾特性。
對於AR(p)過程,當k≤p時,
≠0;當k>p時;
=0。偏自相關函式在滯後期p以後有截尾特徵,因此可用此特徵識別AR(p)過程的階數。
移動平均模型的偏自相關函式
MA(1)過程的偏自相關函式呈指數衰減特徵。若θ1>0,偏自相關函式呈交替改變符號式指數衰減;若θ1<0,偏自相關函式呈負數的指數衰減,如2所示。
對於MA(2)過程,若
的根是實數,偏自相關函式由兩個指數衰減形式疊加而成。若
的根是虛數,偏自相關函式呈正弦衰減特徵(拖尾特徵)。
1>0" style="float: none; display: block; margin: 0px auto; clear: both;" picsrc="9345d688d43f879471d692dade1b0ef41bd53a1d" data-layout="blockcenter" width="449" height="288" url="https://gss1.bdstatic.com/-vo3dSag_xI4khGkpoWK1HF6hhy/baike/s%3D220/sign=58a524d745540923ae69647ca259d1dc/9345d688d43f879471d692dade1b0ef41bd53a1d.jpg" compressw="220" compressh="141" useredit="1" />

1<0" style="float: none; display: block; margin: 0px auto; clear: both;" picsrc="0b7b02087bf40ad14bc01d175b2c11dfa9ecce1a" data-layout="blockcenter" width="458" height="290" url="https://gss1.bdstatic.com/9vo3dSag_xI4khGkpoWK1HF6hhy/baike/s%3D220/sign=62e21429a764034f0bcdc5049fc27980/0b7b02087bf40ad14bc01d175b2c11dfa9ecce1a.jpg" compressw="220" compressh="139" useredit="1" />

因為任何一個可逆的MA(q)過程都可以轉換成一個無限階的、係數按幾何遞減的AR過程,所以MA(q)過程的偏自相關函式呈緩慢衰減特徵,稱拖尾特徵。
ARMA(p,q)過程的偏自相關函式
ARMA(p,q)過程的偏自相關函式也是無限延長的,其表現形式與MA(q)過程的偏自相關函式相類似。根據模型中移動平均分量的階數q以及參數
(i= 1,2,...,q)的不同,偏自相關函式呈指數衰減和(或)正弦衰減混合形式。
對於時間序列數據,偏自相關函式通常是未知的。估計的偏自相關函式
稱為偏相關圖。其中
是對式(1)中
的估計。偏相關圖是由k個估計的偏自相關係數組成的係數列。對於分析非季節序列的偏相關圖,實際中取k=15就足可以了。
所以在觀察偏相關圖時,若
的絕對值超過
(2個標準差),就被認為顯著不為零。
因為AR過程和ARMA過程中AR分量的偏自相關函式具有截尾特徵,所以可利用偏相關圖估計自回歸過程的階數p。偏相關圖是識別AR過程和ARMA過程中AR分量階數的一個重要方法。







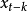
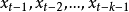















 圖1(b)AR(1)過程的偏自相關函式圖(φ11<0)
圖1(b)AR(1)過程的偏自相關函式圖(φ11<0)