基本介紹
- 中文名:倍長中線
- 外文名:method of times the length of line
- 思想方法:構造全等三角形
- 目的:證明邊之間的關係
- 領域:數學平面幾何
定義,例題,
定義
“倍長中線”是指加倍延長中線,使所延長部分與中線相等,然後往往需要連線相應的頂點,則對應角對應邊都對應相等。常用於構造全等三角形。中線倍長法多用於構造全等三角形和證明邊之間的關係(通常用“SAS”證明)(註:一般都是原題已經有中線時用,不太會有自己畫中線的時候)。
例題
例1:如圖,在△ABC中,AD⊥AC,AB=2AC,AD平分BC,求∠BAC的度數。
解:延長AD到E,使AD=DE。連線BE。
∵AD⊥AC(已知),
∴∠EAC=90°(垂直定義)。
∵AD平分BC(已知),
∴DB=DC(三角形中線定義)。
在△ADC和△EDB中,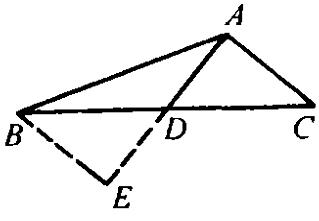 例1-圖
例1-圖
 例1-圖
例1-圖DA=DE(已作),
∠ADC=∠BDE(已證),
DB=DC(已證),
∴△ADC≌△EDB(S.A.S)。
∴AC=BE(全等三角形對應邊相等)。
∴∠E=∠EAC=90°(全等三角形對應角相等)。
∵AB=2AC(已知),
∴AB=2BE(等量代換)。
即AB/2=BE。
∴∠BAE=30°(一條直角邊等於斜邊的一半的直角三角形,這條直角邊所對的角為30°)。
∴∠BAC=∠BAE+∠EAC=30°+90°=120°(等式性質)。
例2:如圖,在△ABC中,AB=5a,AC=3a(a>0),求中線AD的取值範圍。
解:延長AD至AE,交BC於D,使DE=AD。連線EC。
∵∠EDC和∠BDA是對頂角,
∴∠EDC=∠BDA。
又∵D是BC的中點,
∴BD=DC。
在△ABD和△CDE中:
DE=AD,
∠EDC=∠BDA,
BD=DC,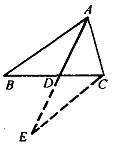 例2-圖
例2-圖
 例2-圖
例2-圖∴△ABD≌△CDE(SAS)。
∴AB=EC=5a。
∵△ACE,
∴AC+EC>AE>EC-AC。
又∵AC=3a,EC=5a,
∴AE的取值範圍為:5a+3a>AE>5a-3a。
即8a>AE>2a。
由題意得:AE=2AD,
∴8a>2AD>2a。
即4a>AD>a。

