對頂角

對頂角（vertical angles, opposite angles)即如果一個角的兩邊分別是另一個角兩邊的反向延長線，且這兩個角有公共頂點，那么這兩個角是對頂角·對頂角的範圍介於0度到180度之間，0度和180度不算在內。對頂角是具有特殊位置的兩個角，對頂角相等反映的是兩個角之間的大小關係。

基本介紹

• 中文名：對頂角
• 外文名：vertical angles, opposite angles
• 適用領域：幾何學、數學
• 範圍：0度~180度（不包括0度和180度）
• 性質：互為對頂角的兩個角相等
• 反映問題：兩個角之間的大小關係

定義

在幾何學中，對頂角是兩個角之間的一種位置關係。兩條直線相交時會產生一個交點，並產生以這個交點為頂點的四個角。稱其中不相鄰的兩個角互為對頂角。或者說，其中的一個角是另一個的對頂角。

對頂角滿足下列定理：兩直線相交，對頂角相等。

用數學語言描述就是：

• 設直線AD、BC交於點O。則形成四個角：∠AOB、∠COD、∠AOC、∠BOD。其中，∠AOB和∠COD互為對頂角，∠AOC和∠BOD互為對頂角。∠AOB = ∠COD，∠AOC = ∠BOD。

例子

如圖1， 兩條直線相交，構成兩對對頂角。∠1與∠3為一對對頂角，∠2與∠4為一對對頂角。

圖1

注意：

1.對頂角一定相等，但是相等的角不一定是對頂角。

2.對頂角必須有共同頂點。

3.對頂角是成對出現的。

在證明過程中使用對頂角的性質時，以 圖1為例，

∴∠1=∠3，∠2=∠4(對頂角相等)。

巧算對頂角

任何兩條直線可以看成一個組合，這樣的組合有C(n，2)=n(n-1)/2 ，每個組合有兩對對頂角 ，因此n條直線相交於一點，共有2C(n，2)=n(n-1)對。即：

2條直線相交於一點，有(2)對不同的對頂角；

3條直線相交於一點，有(6)對不同的對頂角；

4條直線相交於一點，有(12)對不同的對頂角；

..............

n條直線相交於一點，有n(n-1)對不同的對頂角。

性質

如果兩個角是對頂角，那么這兩個角相等。

在同一平面內，互為對頂角的兩個角相等。

歷史

勒斯生於希臘，是一位擅長於幾何學的數學家及哲學家。他一生髮現了多個幾何學定理，包括等腰三角形中的“等邊對等角”定理，也包括對頂角定理。

對頂角定理

設直線AD、BC交於點O，那么，∠AOB和∠AOC 互為鄰補角。根據鄰補角的性質，

其中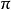是一個平角的弧度數。

類似地，∠COD和∠AOC 互為鄰補角。根據鄰補角的性質，

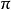
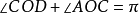
因此，

兩邊減去相同的角度 後，就得到

。

同樣地，可以證明。

用途

對頂角通常用於測量角度以及證明全等三角形。以下是一個利用對頂角證明全等三角形的例子：

如右圖，已知AB=CD，∠BAE=∠CAE。求證：。

證明：在△ABE與△DCE中，

因此，。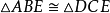

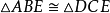
在以上證明中，∠AEB=∠CED的結論就是通過對頂角定理得出的。注意，在一般的幾何證明中，對頂角定理並不需要顯式地敘述出來，可以當作是默認的條件。