基本介紹
判定一
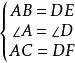
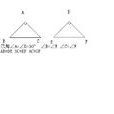
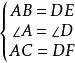
≌ 編輯 鎖定 討論999 性質:全等圖形形狀大小(即周長、面積、邊長、腰長以及所有對應角、對應邊、角度與長度)完全相同。全等是相似的一種特例。當相似比為1時,...
《≌ 醉夢人≌》是雲樓墨雨創作的網路小說,發表於晉江文學網。...... 《≌ 醉夢人≌》是雲樓墨雨創作的網路小說,發表於晉江文學網。中文名稱 ≌ 醉夢人≌ 作...
愛≌0編輯 鎖定 本詞條缺少名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!鄭秀文的一首歌曲,闡述了愛的執著與傷害。 具體歌詞如下: ...
《≌神愛≌》是雲樓墨雨創作的言情小說,發表於晉江文學網。...... 《≌神愛≌》是雲樓墨雨創作的言情小說,發表於晉江文學網。中文名稱 ≌神愛≌ 作者 雲樓...
《≌塔羅牌情人≌》是雲樓墨雨創作的網路小說,發表於晉江文學網。...... 《≌塔羅牌情人≌》是雲樓墨雨創作的網路小說,發表於晉江文學網。 中文名稱 ≌塔羅牌情...
《≌百合半香≌》是雲樓墨雨創作的純愛小說,發表於晉江文學網。...... 《≌百合半香≌》是雲樓墨雨創作的純愛小說,發表於晉江文學網。中文名稱 ≌百合半香≌ ...
《≌ 蝶游 ≌》是雲樓墨雨創作的網路小說,發表於晉江文學網。...... 《≌ 蝶游 ≌》是雲樓墨雨創作的網路小說,發表於晉江文學網。 中文名稱 ≌ 蝶游 ≌ ...
《≌絕舞涼州≌》是雲樓墨雨創作的言情小說,發表於晉江文學網。...... 《≌絕舞涼州≌》是雲樓墨雨創作的言情小說,發表於晉江文學網。中文名稱 ≌絕舞涼州≌ ...
“≌”是全等號,“∥”是平行符號,“⊥”是垂直符號,“∝”是正比例符號(表示反比例時可以利用倒數關係),“∈”是屬於符號,“⊆”是包含於符號,“⊇”是...
全等於“≌”表示兩個圖形能完全重合(包括形狀和面積)...... 全等於“≌”表示兩個圖形能完全重合(包括形狀和面積) 中文名 全等於 外文名 identically equal to...
